剪切模量
剪切應力與應變的比值
剪切模量(modulus of rigidity),材料常數,是剪切應力與應變的比值。又稱切變模量或剛性模量。材料的力學性能指標之一。是材料在剪切應力作用下,在彈性變形比例極限範圍內,切應力與切應變的比值。
剛度參數γ,所使用的混凝土的剪切模量G可取等於0.425E,E是混凝土的彈性模量。剪切模量G和彈性模量E、泊松比μ之間有關係:G=E/(2(1+μ))。

剪切模量

測量剪切模量的儀器
本文試驗用料均為人工開採的堆石料,根椐實際工程設計級配要求和三軸儀試樣直徑模擬的試料級配曲線如圖1所示。其中,公伯峽堆石壩的3種主堆石料採用的是同一種級配曲線。表1列出各試料的岩性、平均粒徑、不均勻係數、初始孔隙比以及圍壓等試驗條件。除了瀑布溝和關門山堆石料外,其它堆石料的試驗均在等向固結條件下進行,振動時採用不排水狀態。試樣製備採用分層壓實法,試驗振動頻率均為0.1Hz.
土的非線性性質通常採用等效線性模型,即把土視為粘彈性體,用等效動彈模Eeq(或動剪切模量Geq)和等效阻尼比h這兩個參數來反映土的動應力-應變關係的非線性和滯后性,並把它們表示為動應變幅的函數。需要指出,試驗中每級荷載振動12~15次,不同的加荷周次實測的應力-應變滯回曲線多少有一些差別,由此算出的等效動彈模和阻尼比也不完全一樣。因此,在分析整理試驗成果時,軸嚮應變、等效動彈模以及阻尼比均以第3次至第10次的平均值給出。
2.1 最大等效動彈模(Eeq)max的確定
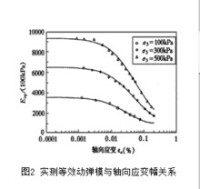
圖二
2.2 最大等效動剪切模量有效應力
實測最大等效動彈模(E)max與平均有效應力σ在對數坐標下可以近似地直線關係,表示為
(E)=kσm (1)
式中:k是等效彈模係數,n是模量指數,E和σ的單位是kPa。
為了便於比較,將最大等效動彈模(E)換算成最大等效動剪切模量(G),並引入F(e)以消除孔隙比的影響,於是最大等效動剪切模量可表示為
(G)=AF(e)σm (2)
式中:A為等效剪切模量係數;e為孔隙比;F(e)=(2.17-e)/(1+e)是孔隙比函數;(G)為最大等效動剪切模量,(G)=(E)/2(1+μ),其中泊桑比μ根據試驗條件取值,即不排水狀態取0.5.剪應變γ與軸嚮應變ε的關係為
γ=ε(1+μ) (3)

表二
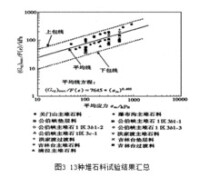
圖三
2.3現場彈性波試驗與室內三軸試驗
結果比較70年代末80年代初,日本電力中央研究所對日本的5座不同岩質的堆石壩進行了彈性波試驗並將其試驗結果與室內大型三軸試驗進行過比較,日本建設省土木研究所曾對三保和七宿兩座堆石壩進行過現場彈性波試驗和室內大型三軸試驗。筆者等對我國關門山面板堆石壩進行了現場彈性波試驗並與文獻做過比較分析。本文將再次引用這些成果,將室內試驗測得的13種堆石料的平均最大等效動剪切模量及其上、下包線按下式換算成剪切波速進行比較
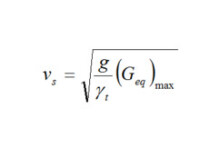
剪切模量
式中:g是重力加速度,9.81m/s;γ是堆石體密度,t/m;最大等效動剪切模量(G)的單位應換算成t/m;剪切波速v的單位是m/s。
需要說明,式(2)中的平均有效應力 σ=1/3(1+μ)(1+K)γ (6)
式中:泊松比μ取0.35,主應力比K取1.5,z為深度m。
圖4是現場彈性波試驗與室內三軸試驗結果比較,其中曲線4是本文圖3中建議的平均線方程,曲線5和曲線6分別是圖3中的上包線和下包線。曲線7是關門山面板壩現場彈性波試驗成果。

圖四
2.4 歸一化剪應變幅γ關係
圖5給出歸一化等效動剪切模量隨動剪應變幅的依賴關係的典型實例,即吉林台與洪家度兩座面板堆石壩主堆

圖五
為了對各種堆石料的試驗結果進行比較,將作者用本文方法測得的各種堆石料的歸一化等效動剪切模量與動剪應變幅的依賴關係匯總於圖6.圖中每條曲線表示一種試驗堆石料G/(G)~γ變化範圍的平均值。從圖中結果可以看出,儘管這些堆石料的岩性和級配等有較大差別,且最大等效動剪切模量的變化範圍也較大,但各種堆石料的歸一化等效動剪切模量與動剪應變幅的依賴關係的離散性並不大。為便於應用,本文將圖6中各種堆石料的試驗結果再做平均處理,建議了一般堆石料歸一化等效動剪切模量與動剪應變幅依賴關係的取值範圍如圖7所示。

圖6 、7、 8、 9
大量的研究表明,動剪切模量越高等效阻尼比就越低,等效阻尼比不僅隨動剪應變幅γ的增大而增加,而且還與圍壓σ或平均有效應力σ有關,在相同的動剪應變幅情況下,圍壓σ增大,等效阻尼比減小。此外,固結應力比K對等效阻尼比也有影響,即在相同的圍壓σ及動剪應變幅情況下,固結應力比K增加則等效阻尼比減小。本文匯總了各種堆石料的等效阻尼比與動剪應變幅的關係如圖8,圖中每條曲線即代表一種試驗堆石料的h~γ變化範圍的平均值。可以看出,各種堆石料的等效阻尼比隨動剪應變幅變化的離散度比歸一化等效動剪切模量隨動剪應變幅變化的離散度要大一些。圖9是將圖8中各種堆石料的試驗結果再做平均處理,建議一般堆石料等效阻尼比與動剪應變幅依賴關係的取值範圍。總體上看,堆石料的等效阻尼比不高,當動剪應變幅γ=10時,等效阻尼比約2%左右,γ=10時,等效阻尼比接近5%,而當動剪應變幅大於γ=10后,阻尼比上升得較快,這說明堆石料進入較強的非線性,應變滯後於應力的現象越加明顯。需要指出,等效阻尼比的離散範圍比較大,這一方面是堆石料本身含有的不確定性引起,另一方面也與試驗數據的分析整理方法有關。
(1)本文依據室內高精度大型三軸試驗給出的十餘種堆石料最大等效動剪切模量的估算公式與國內外8座堆石壩現場彈性波試驗結果基本吻合,由此說明,儘管堆石壩築壩材料的級配、初始孔隙比、岩性以及風化程度等不盡相同,但由於採用重型碾機械化施工,現代堆石壩的實際填築密度較高,壩體內剪切波速分佈也大體接近。
(2)在尚未取得堆石料試驗數據的情況下進行堆石壩地震反應分析,可參考本文圖3和圖4粗略估計最大等效動剪切模量,參考圖7和圖9確定歸一化等效動剪切模量、等效阻尼比與動剪應變幅的關係。選取計算參數時應主要考慮岩質硬度、靜抗剪強度等對最大等效動剪切模量以及衰減關係的影響。應該說,按本文建議公式或給出的範圍估算,可以滿足工程需要。
(3)與粘土和砂相比,築壩堆石料的試驗設備和試驗技術方面都存在許多的困難,迄今為止,有關堆石料的動剪切模量和阻尼比方面的試驗資料尚不多見,作者將進一步積累資料做深入地研究。
材料在外力作用下發生變形。當外力較小時,產生彈性變形。彈性變形是可逆變形,卸載時,變形消失並恢復原狀。在彈性變形範圍內,其應力與應變之間保持線性函數關係,即服從虎克(Hooke)定律:
彈性模量是表徵晶體中原子間結合力強弱的物理量,故是組織結構不敏感參數。在工程上,彈性模量則是材料剛度的度量。
實際上,理想的彈性體是不存在的,多數工程材料彈性變形時,可能出現載入線與卸載線不重合、應變滯後於應力變化等彈性不完整性。彈性不完整性現象包括包申格效應、彈性後效、彈性滯后和循環韌性等。
對非晶體,甚至對某些多晶體,在較小的應力時,可能會出現粘彈性現象。粘彈性變形是既與時間有關,又具有可恢復的彈性變形,即具有彈性和粘性變形兩方面特徵。粘彈性變形是高分子材料的重要力學特性之一。
當施加的應力超過彈性極限時,材料發生塑性變形,即產生不可逆的永久變形。通過塑性變形,不但可使材料獲得預期的外形尺寸,而且可使材料內部組織和性能產生變化。
單晶體塑性變形的兩個基本方式為滑移和孿生。滑移和孿生都是切應變,而且只有當外加切應力分量大於晶體的臨界分切應力tC時才能開始。然而,滑移是不均勻切變,孿生為均勻切變。
對於多晶體而言,要求每個晶粒至少具備由5個獨立的滑移系才能滿足各晶粒在變形過程中相互制約和協調。多晶體中,在室溫下晶界的存在對滑移起阻礙作用,而且實踐證明,多晶體的強度隨其晶粒細化而提高,可用著名的Hall-Petch公式來加以描述。
金屬彈簧材料種類繁多,大量使用的是彈簧鋼。在選用彈簧鋼進行彈簧設計計算時,要用到材料的切變模量或彈性模量。國內外幾乎所有的設計資料和有關教科書以及GB/T1239.6-92《圓柱螺旋彈簧設計計算》等對金屬彈簧材料的切變模量都以定值給出。但其中的圓柱螺旋彈簧、蝸卷彈簧、非線性特性線螺旋彈簧、多股螺旋彈簧等,如按上述傳統設計資料中給出的切變模量取值,那麼,計算的彈簧變形量與其實際測量的變形量有較大的誤差。現以我廠生產的NYL-2000型壓力試驗機上使用的測力彈簧為例試述如下。
1 設計計算的彈簧伸長量與實測伸長量
大、小測力彈簧(由上海中國彈簧廠加工)是普通圓柱螺旋拉伸彈簧。彈簧材料為60Si2MnA,熱處理45~50HRc。其部分設計參數如表1。
表一
眾所周知,由於加工后的成品彈簧,特別是熱繞成形並需經熱處理的彈簧,不可避免地存在著一定的尺寸偏差。如彈簧鋼絲直徑、彈簧中徑等都可能與設計時的參數不同,甚至偏差很大。這就導致了彈簧的實際伸長量與設計計算的伸長量存在著一定的誤差。表2就是筆者根據檢驗時測量的彈簧的有關尺寸,再按傳統的材料切變模量取值計算的伸長量與其實際測量的伸長量比較。

表二
2 熱處理后的彈簧鋼的切變模量
為了使彈簧能獲得較高的屈服極限、彈性極限、高的屈強比和疲勞強度,彈簧一般都要經過熱處理。而經過熱處理的彈簧材料的彈性模量和切變模量卻發生了變化。其中,切變模量變化較大,如常用的彈簧鋼60Si2MnA經過淬火和不同溫度回火處理的彈性模量和切變模量抄於表3。
表三
3 取熱處理后的切變模量值計算的彈簧伸長量與其實測值比較
如取表3中450℃回火后的切變模量值83160MPa,硬度約為47HRc,再按表2中測力彈簧的實測尺寸代入公式計算的結果列於表4。

表四
至於合金為單相固溶體時,由於溶質原子存在會呈現固溶強化效果,對某些材料還會出現屈服和應變時效現象;當合金為多相組織結構時,其變形還會受到第二相的影響,呈現彌散強化效果。
而陶瓷晶體,由於其結合鍵(離子鍵、共價鍵)的本性,再加上陶瓷晶體中的滑移系少,位錯的b大,故其塑性變形相對金屬材料要困難得多,只有以離子鍵為主的單晶陶瓷才能進行較大的塑性變形。對於高分子材料,其塑性變形是靠粘性流動而不是靠滑移產生的,故與材料粘度密切相關,而且受溫度影響很大。
材料經塑性變形后,外力所做的功部分以儲存能形式存在於材料內部,從而使系統的自由能升高,處於不穩定狀態。故此,回復再結晶是材料經過冷變形后的自發趨勢,加熱則加快這一過程的發生。
當加熱溫度較低,時間較短時,發生回復。此時,主要表現為亞結構的變化和多邊化過程,第一類內應力大部消除,電阻率有所下降,而對組織形態和力學性能影響不大。
當加熱溫度較高,時間較長時就發生再結晶現象。再結晶時,新的無畸變等軸晶將取代冷變形組織,其性能基本上回復到冷變形前的狀態。
再結晶完成後繼續加熱時,晶粒將發生長大現象。
