等周問題
1901年赫爾維茨提出的概念
P若為封閉曲線的周界長,A為曲線所包圍的區域面積,
雖然等周定理的結論早已為人所知,但要嚴格的證明這一點並不容易。首個嚴謹的數學證明直到19世紀才出現。之後,數學家們陸續給出了不同的證明,其中有不少是非常簡單的。等周問題有許多不同的推廣,例如在各種曲面而不是平面上的等周問題,以及在高維的空間中給定的“表面”或區域的最大“邊界長度”問題等。
在物理中,等周問題和跟所謂的最小作用量原理有關。一個直觀的表現就是水珠的形狀。在沒有外力的情況下(例如失重的太空艙里),水珠的形狀是完全對稱的球體。這是因為當水珠體積一定時,表面張力會迫使水珠的表面積達到最小值。根據等周定理,最小值是在水珠形狀為球狀時達到。
等周問題
等周問題
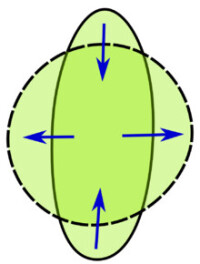
平面上的等周問題是等周問題最經典的形式,它的出現可以追溯到很早以前。這個問題可以被表述為:在平面上所有周長一定的封閉曲線中,是否有一個圍成的面積最大?如果有的話,是什麼形狀?另一種等價的表述是:當平面上的封閉曲線圍成的面積一定時,怎樣的曲線周長最小?
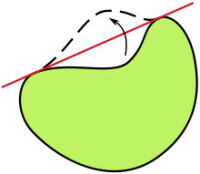
雖然圓看似是問題的表面答案,但證明此事實其實不易。首個接近答案的步驟出現在1838年——雅各·史坦納以幾何方法證明若答案存在,答案必然是圓形。不久之後他的證明被其他數學家完善。
其方法包括證明了不完全凸的封閉曲線的話,能以“翻折”凹的部分以成為凸的圖形,以增加面積;不完全對稱的封閉曲線能以傾斜來取得更多的面積。圓,是完全凸和對稱的形狀。可是這些並不足以作為等周定理的嚴格證明。
2012年,潘憶思利用不等式給出了一個十分簡單初等證明。論文名稱《不等式與等周問題》。