根軌跡法

，..提求征根簡單，且控制系 統析設計廣泛。求征程，圖示征程根系統某參值系，參取值，征根述系圖找。根軌跡。根軌跡具觀，系統根軌跡析構參閉環系統穩瞬態響，析參化系統影響。設計線控制系統，根據系統指標求確調整參及系統環零極置，即根軌跡系統析綜合。

根軌跡析設計閉環控制系統的圖解方法。特徵方程（見傳遞函數）的根隨某個參數由零變到無窮大時在複數平面上形成的軌跡，稱為根軌跡。在控制系統的分析中，對特徵方程根的分佈的研究，具有重要的意義。當特徵方程的次數不高於2時，其根可用解析方法來簡單地定出；但當特徵方程的次數高於 2時，求根過程將變得相當複雜。美國學者W.R.埃文斯在1948年提出的根軌跡方法，為簡化特徵方程的求根過程提供了一種有效的手段。在把根軌跡技術應用於控制系統的分析時，常取系統的開環增益為可變參數，據此作出的根軌跡，表示閉環控制系統的極點在不同開環增益值下的分佈。控制系統的極點在複數平面上的位置與系統的穩定性和過渡過程性能有密切的關係。根軌跡的建立，為分析控制系統在不同開環增益值時的行為提供了方便的途徑。對於設計控制系統的校正裝置(見控制系統校正方法)，根軌跡法也是基本方法之一。根軌跡法和頻率響應法被認為是構成經典控制理論的兩大支柱。

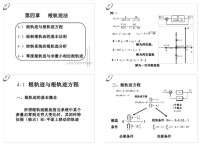
圖控制系統，G(s)和H(s)分別表示系統前饋通道和反饋通道中部件的傳遞函數，並且當s=0時它們的值均為1,而K表示系統的開環增益，則控制系統的根軌跡條件可表示為：

相角條件　開環傳遞函數KG(s)H(s)的相角值

{KG(s)H(s)}=±180º(2k+1)　(k=0,1,2,…)

幅值條件　開環傳遞函數KG(s)H(s)的模

│KG(s)H(s)│=1 系統的根軌跡，就是當開環增益K由零變化到無窮大時，由滿足相角條件和幅值條件的 s值在複數平面上所構成的一組軌跡。

在控制系統的分析和綜合中，往往只需要知道根軌跡的粗略形狀。由相角條件和幅值條件所導出的 8條規則，為粗略地繪製出根軌跡圖提供方便的途徑。

①　根軌跡的分支數等於開環傳遞函數極點的個數。

②　根軌跡的始點（相應於K=0）為開環傳遞函數的極點，根軌跡的終點（相應於K=∞）為開環傳遞函數的有窮零點或無窮遠零點。

③　根軌跡形狀對稱於坐標系的橫軸（實軸）。

④　實軸上的根軌跡按下述方法確定：將開環傳遞函數的位於實軸上的極點和零點由右至左順序編號，由奇數點至偶數點間的線段為根軌跡。

⑤　實軸上兩個開環極點或兩個開環零點間的根軌跡段上，至少存在一個分離點或會合點，根軌跡將在這些點產生分岔。

⑥　在無窮遠處根軌跡的走向可通過畫出其漸近線來決定。漸近線的條數等於開環傳遞函數的極點數與零點數之差。

⑦　根軌跡沿始點的走向由出射角決定，根軌跡到達終點的走向由入射角決定。

⑧　根軌跡與虛軸（縱軸）的交點對分析系統的穩定性很重要，其位置和相應的K值可利用代數穩定判據來決定。

圖2是按照上述規則畫出的一些典型的根軌跡圖。

根軌跡的精確化 在有些情況下，有必要對按基本規則畫出的根軌跡的粗略形狀，特別是位於虛軸附近的部分，進行修正，使之精確化。實現精確化的一條比較簡便的途徑，是採用一種由埃文斯設計的所謂對數螺旋尺的專用工具。

根軌跡的計算機輔助製圖 70年代以來，隨著電子計算機的普及，利用計算機對根軌跡的輔助製圖的演演算法和程序都已建立，這大大減輕了系統分析和設計人員的繁重工作。

根軌跡的應用主要有三個方面。

①　用於分析開環增益(或其他參數)值變化對系統行為的影響：在控制系統的極點中，離虛軸最近的一對孤立的共軛複數極點對系統的過渡過程行為具有主要影響，稱為主導極點對。在根軌跡上，很容易看出開環增益不同取值時主導極點位置的變化情況，由此可估計出對系統行為的影響。

②　用於分析附加環節對控制系統性能的影響：為了某種目的常需要在控制系統中引入附加環節，這就相當於引入新的開環極點和開環零點。通過根軌跡便可估計出引入的附加環節對系統性能的影響。

③　用於設計控制系統的校正裝置：校正裝置是為了改善控制系統性能而引入系統的附加環節，利用根軌跡可確定它的類型和參數設計。