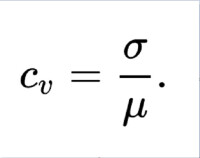離散係數
統計學當中的常用統計指標
離散係數又稱變異係數,是統計學當中的常用統計指標。離散係數是測度數據離散程度的相對統計 量,主要是用於比較不同樣本數據的離散程度。離散係數大,說明數據的離散程度也大;離散係數小,說明數據的離散程度也小。
離散係數是衡量資料中各觀測值離散程度的一個統計量。當進行兩個或多個資料離散程度的比較時,如果度量單位與平均數相同,可以直接利用標準差來比較。如果單位和(或)平均數不同時,比較其離散程度就不能採用標準差,而需採用標準差與平均數的比值(相對值)來比較: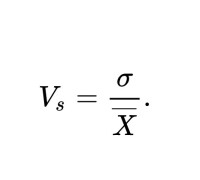
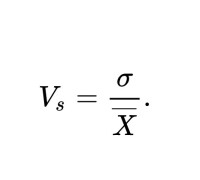
離散係數
表示總體離散係數和樣本離散係數
離散係數通常可以進行多個總體的對比,通過離散係數大小的比較可以說明不同總體平均指標(一般來說是平均數)的代表性或穩定性大小。一般來說,離散係數越小,說明平均指標的代表性越好;離散係數越大,平均指標的代表性越差。
離散係數只對由比率標量計算出來的數值有意義。舉例來說,對於一個氣溫的分佈,使用開爾文或攝氏度來計算的話並不會改變標準差的值,但是溫度的平均值會改變,因此使用不同的溫標的話得出的變異係數是不同的。也就是說,使用區間標量得到的變異係數是沒有意義的。
極差(全距)係數:Vr=R/X’ ;
平均差係數:Va,d=A.D/X’
方差係數:V方差=方差/X’ ;
標準差係數:V標準差=標準差/X’(其中,X’表示X的平均數。)
用途和意義
離散係數反映單位均值上的離散程度,常用在兩個總體均值不等的離散程度的比較上。若兩個總體的均值相等,則比較標準差係數與比較標準差是等價的。
一組數據的標準差與其相應的均值之比,是測度數據離散程度的相對指標,其作用主要是用於比較不同組別數據的離散程度。其計算公式為v=S/(X的平均值)。
標準變異係數是一組數據的變異指標與其平均指標之比,它是一個相對變異指標。
離散係數(coefficient of variation)只在平均值不為零時有定義,而且一般適用於平均值大於零的情況。變異係數也被稱為標準離差率或單位風險。
由於指數分佈的標準差等於其平均值,所以它的離散係數等於一。離散係數小於一的分佈,比如愛爾朗分佈稱為低差別的,而離散係數大於一的分佈,如超指數分佈則被稱為高差別的。
優點
比起標準差來,離散係數的好處是不需要參照數據的平均值。離散係數是一個無量綱量,因此在比較兩組量綱不同或均值不同的數據時,應該用變異係數而不是標準差來作為比較的參考。
缺點
● ● 當平均值接近於0的時候,微小的擾動也會對離散係數產生巨大影響,因此造成精確度不足。
● ● 離散係數無法發展出類似於均值的置信區間的工具 。
離散係數反映單位均值上的離散程度,其計算公式為
離散係數
在對比情況下,離散係數較大的其分佈情況差異也大。