點陣
點陣
晶體的基本特徵是其內部結構的周期性,那麼很自然就應當把原子排列與空間的網點陣列聯繫起來。後者稱為空間點陣,或簡稱為點陣。點陣中各個點的環境是彼此相同的。
點陣
點陣
19世紀出現了布喇菲(A.Bravais)的空間點陣學說,這一學說能解釋有理指數定律和晶面角守恆定律,但它只是合理的猜想,其正確性到1912年才被勞厄(Laue,MaxTheodorFelixyon)等人的x射線衍射實驗證實。幾十年來的研究已探明了成千上萬的晶體結構,肯定了晶體的周期性。
晶體中原子或原子團在三維空間有規律的周期排列構成了晶體結構。為了研究方便,人們忽略了那些種類繁多的原子和原子團,而把晶體看成是一些幾何點在空間有規律的周期排列,同時,這些點與實際晶體中的原子又具有某種固定的空間位置關係。
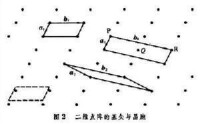
設想在空間有一組平行的等距離平面,與另外一組等距離平面相交,然後,它們又與第三組等距離的平行平面相交。結果,兩兩面相交的交線便構成了空間分佈的格子,而交線的相交點便是空間分佈的點,這些空間周期分佈的點構成空間點陣。其中每個陣點的周圍環境都相同,這就是說,每個陣點周圍的陣點數以及各陣點相對參考點的取向相同。
點陣中的平行六面體稱為陣胞。實際上,有許多種方式取平行六面體作為陣胞。描述陣胞的形狀和大小採用3個矢量,即若以陣胞某角點為原點,沿3個棱邊作3個矢量;通常面對的為a,向右為b,向上為c。它們之間的夾角分別為α,β和γ,稱a、b、c和α,β和γ為陣胞的點陣參數。陣胞是點陣的基本單元,借陣胞的無限平移可以得到整個點陣。
空間點陣的類型可以用皮爾遜(Pearson)符號表示,該符號中第一個為小寫字母,代表所屬晶系;第二個為大寫字母,代表點陣類型。注意菱方晶系的晶胞是簡單晶胞,但卻用R作為其點陣類型符號。
| 晶系 | 符號 | 點陣類型 | 符號 |
| 三斜 | a | 簡單 | P |
| 單斜 | m | 底心 | C |
| 正交 | o | 體心 | I |
| 六方 | h | 面心 | F |
| 四方 | t | 菱方 | R |
| 立方 | c |
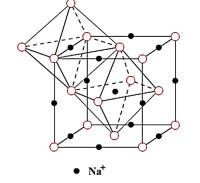
在固體物理學中,一般選取空間點陣中體積最小的平行六面體作為單胞,這樣的單胞只能反映其空間點陣的周期性,但不能反映其對稱性。如面心立方點陣的固體物理單胞並不反映面心立方的特徵。
點陣
由於固體物理單胞只能反映晶體結構的周期性,不能反映其對稱性,所以在晶體學中,規定了選取單胞要滿足以下幾點原則:
①要能充分反映整個空間點陣的周期性和對稱性;
②在滿足①的基礎上,單胞要具有儘可能多的直角;
③在滿足①、②的基礎上,所選取單胞的體積要最小。
根據以上原則,所選出的14種布拉菲點陣的單胞可以分為兩大類。一類為簡單單胞,即只在平行六面體的8個頂點上有結點,而每個頂點處的結點又分屬於8個相鄰單胞,故一個簡單單胞只含有一個結點。另一類為複合單胞(或稱複雜單胞),除在平行六面體頂點位置含有結點之外,尚在體心、面心、底心等位置上存在結點,整個單胞含有一個以上的結點。14種布拉菲點陣中包括7個簡單單胞,7個複合單胞。
點陣
簡單點陣:a、b、c;
底心點陣:a、b、c、(a+b)/2;
體心點陣:a、b、c、(a+b+c)/2;
面心點陣:a、b、c、(a+b)/2、(b+c)/2、(a+c)/2;
所以布拉菲點陣也稱為平移點陣。
點陣字體是把每一個字元都分成16×16或24×24個點,然後用每個點的虛實來表示字元的輪廓。點陣字體優點是顯示速度快,不像矢量字體需要計算;其最大的缺點是不能放大,一旦放大后就會發現文字邊緣的鋸齒。

點陣

