籌算
中國古代的計算方法之一
籌算是中國古代的計算方法之一,以刻有數字的算籌記數、運算,約始於春秋,直至明代才被珠算代替。
籌算
chóu suàn
ㄔㄡˊ ㄙㄨㄢˋ
[count] 古代計算方法之一,用刻有數字的竹籌來計算數目。亦稱“籌策”。
又因向聞此地素精籌算,要去訪訪來歷。——《鏡花緣》
1、亦作“籌筭”。古時刻有數字的竹籌。
《漢書·貨殖傳》:“致之 臨卭,大憙,即鐵山鼓鑄,運籌算。”
晉 葛洪 《抱朴子·雜應》:“仰觀天文,俯察地理,占風氣,布籌筭。”
南朝 宋 劉義慶 《世說新語·文學》:“重問曰:‘聖人如柱邪?’ 王 曰:‘如籌筭。雖無情,運之者有情。’”
2. 謀划計算。
《隋書·李密傳》:“密 多籌算,才兼文武,志氣雄遠,常以濟物為己任。”
《新唐書·李勣傳》:“其用兵多籌算,料敵應變,皆契事機。”
明 沈德符 《野獲編·列朝二·工匠見知》:“而木匠 徐杲 以一人拮据經營,操斤指示,聞其相度時,第四顧籌算,俄頃即出。”
《二十年目睹之怪現狀》第三三回:“我也籌算過來,我們既然沾了手,萬不能半途而廢,一定要弄他個水落石出纔好。”
清 李寶嘉 《官場現形記》第九回:我同你做了知己朋友,總得替你籌算籌算。

籌算
《漢書·律曆志》中有關於算籌的形狀與大小的記載:“其演演算法用竹,徑一分,長六寸,二百七十一枚而成六觚,為一握。”西漢算籌一般是直徑為0.23厘米,長約13.86厘米的圓形竹棍,把二百七十一枚籌捆成六角形的捆。而《隋書·律曆志》稱:“其算用竹,廣二分,長三寸。正策三廉,積二百一十六枚成六觚,乾之策也。負策四廉,積一百四十四枚成方,坤之策也。”到了隋代,算籌已是三棱形與四棱形兩種,以區別正數與負數。其廣約為0.59厘米,長約8.85厘米。這表明從漢到隋,算籌從圓而方,由長變短,以便運用。魏劉徽注《九章算術》稱:“正算赤,負算黑,否則以邪正為異。“又《夢溪筆談》卷八稱:”演演算法用赤籌、黑籌,以別正負之數。“可見早在三國以前,中算家便已用籌的顏色的赤、黑或形狀的邪、正(三棱形和四棱形)來區分正、負數了。

日本古算術中帶格子的算籌碼
籌算
算籌記數的規則,最早載於《孫子算經》:“凡算之法,先識其位。一縱十橫,百立千僵。千、十相望,萬、百相當。”用算籌表示數目有縱、橫兩種方式:中國古代的籌算不僅是正、負整數與分數的四則運算和開方,而且還包含著各種特定籌式的演算。中算家不僅利用籌碼不同的“位”來表示不同的“值”,發明了十進位值制記數法,而且還利用籌在算板上各種相對位置排列成特定的數學模式,用以描述某種類型的實際應用問題。例如列衰、盈朒、“方程”諸術所列籌式描述了實際中常見的比例問題和線性問題;天元、四元及開方諸式,則刻畫了高次方程問題;而大衍求一術則是為“乘率”而設計的特殊籌式。籌式以不同的位置關係表示特定的數量關係。在這些籌式所規定的不同“位”上,可以布列任意的數碼(它們隨著實際問題的不同而取不同的數值),因而,中國古代的籌式本身就具有代數符號的性質。可以認為,是一種獨特的符號系統。中國古代的籌算表現為演演算法的形式,而具有模式化、程序化的特徵。中國的籌算不用運算符號,無須保留運算的中間過程,只要求通過籌式的逐步變換而最終獲得問題的解答。因此,中國古算中的“術”,都是用一套一套的“程序語言”所描寫的程序化演演算法,並且中算家經常將其依據的算理蘊涵於演算的步驟之中,起到“不言而喻,不證自明”的作用。可以說“寓理於算”是古代籌算在表現形式上的又一特點。
算籌是在珠算髮明以前中國獨創並且是最有效的計算工具。中國古代數學的早期發達與持續發展是受惠於籌的。
一種文化穿越了千年,在駢體歌謠般的吟唱聲里把現場所有人的心引進了藏民族特定的智慧里。2011年5月23日,拉薩市政協民族會議室里,專家及學者齊聚一堂,拉薩市檔案館搶救西藏古老籌算文化演算會在這裡召開。

籌算
目前,全市甚至全區知曉和運用該籌算的人已寥寥無幾,為及時搶救西藏古老籌算文化,今天拉薩市檔案館特邀請相關專家舉辦西藏古老籌算演算會,重溫古代的各種度量衡並重新製作籌算器具及計算盤、各種算籌等。在向外界展示同時還要製作各種影像資料加以保存。古西藏的各類度量衡和籌算的產生與運用,表明古西藏的先祖是聰明和智慧的,這種古老的籌算方式產生及運用為西藏的政治、經濟、文化各方面的發展做出了卓越的貢獻,是祖國文化寶庫中藏民族的寶貴文化瑰寶,更是不可再生的歷史檔案。
為了及時搶救這一文化遺產拉薩市檔案館自2010年起就開始走訪原地方政府“孜康勤空”(審計署)工作過的老同志、知曉西藏古老籌算文化的區、市兩級政協委員及自治區社科院諾張伍金先生,西藏大學的有關專家等做了大量工作。拉薩市檔案館搶救西藏古老籌算文化檔案這一舉措,不但豐富了館藏而且也從另一個側面體現了拉薩市檔案館特色館藏的價值。
三位專家在精心演算,觀看的人們更為屏氣凝神,現場沒有一點餘音,只有古樸及歷史久遠的迴響,充溢著所有的空間、白髮學者、古老的演算方式,與是古老與現代發展與傳承在這裡突顯的尤為重要與迫切了。

籌算一到九的直型態與橫型態對照
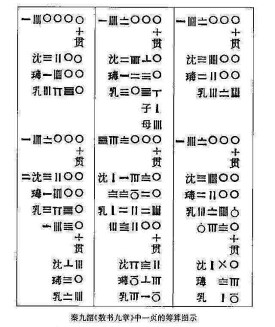
算籌數系是世界上唯一只用一個符號的方向和位置的組合,表示任何十進位數字或分數的系統。單位數字:將籌棍豎排一根棍表示1,兩根棍表示2,5根棍表示5如圖上。但從6至9數字的表示,不是並排6至9根籌棍,而是採用同位五進位,即用一根籌棍代表數碼5,橫放在籌數1至4的上方如圖。這已蘊含算盤雛形。上排是籌算中1至9的豎碼,下排是相應數字的橫碼。
使用直橫排列避免混淆
大於9的數字,則用十進位表示,在個位數的位置左邊,放置一個籌數,代表這個籌數的十倍,在十位數值左的位置,代表百位數,如此類推。如圖所示數二百三十一(231)的表示法,在個位放置一根籌碼,表示1,在十位放置籌數3,代表30,在百位放置籌數2,代表200,總數即二百三十一(231)。《孫子算經》云:
凡算之法:先識其位,一從十橫,百立千僵,千十相望,萬百相當

使用直橫排列避免混淆

孫子算經
。
籌算板一般是桌面或地面,通常沒有格子。如果籌碼2,3,1並排排列,有可能被誤讀為51或24;為了避免鄰位誤讀,先民發明了每隔一位交替使用豎碼橫碼,即個位豎碼,十位用橫碼,百位用豎碼,千位用橫碼,如此類推,就可以完全避免誤讀了。
數字後加斜棍表負數
中國自有籌算起就有“0”,即以空位表示“0”。籌算中的零是位置零和運算結果的零,沒有特定符號。
宋代數學家用紅色籌碼代表正數,用黑色籌碼代表負數,也有一律用黑色籌碼,但在數字最後一位加一根斜棍標示為負數。
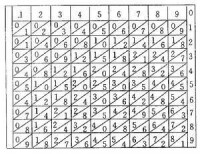
十七世紀初葉,英國數學家耐普爾發明的一種算籌計演演算法。明末介紹到我國,也稱“籌算”。清代梅文鼎、戴震曾加以研究,戴震稱為策算。籌是用竹或木製成的,一至九每籌正反面各分九格,每格斜分為二,個位數寫於斜線下角,十位數寫於斜線上角。第一籌正面寫一至九,第二籌寫一至九各數的二倍的數,第三到第九各籌中,分別寫一至九各數的三倍至九倍的數,第一籌的反面與第九籌同,其他籌類此。第五籌的反面為空。計算時把籌拼攏,進行乘除。清代梅文鼎改斜格為兩半圓合一位格,比較醒目。後來又將橫籌改為縱籌,更為方便。又有平方籌、立方籌等專為開方之用。
籌算
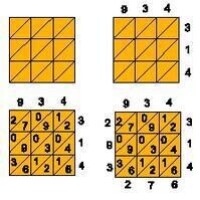
格子演演算法
napier suanchou,亦稱“納皮爾計算尺”。一種能簡化計算的乘法速算器,由英國數學家、對數的發明人納皮 爾發明。如右圖,它由十根木條組成,每根木條上都刻有數碼,右邊第一根木條是固定的,其餘的都可以根據計算的需要進行拼合和調換位置。這種算籌可以用加法和一位數乘法代替多位數的乘法,也可以用除數為一位數的除法和減法代替多位數的除法,從而簡化了計算。其計算原理的“格子乘法”。例如,要計算934×314,首先將9,3,4和3,1,4擺成如下圖所示,遇到對角線上的兩上數字就加在一起,這就容易得到934分別乘以3,1,4的結果為2802,934和3736,然後再錯位相加,就得到所要求的結果293276。這種簡單的計算器,在當時很受歡迎,流行了許多年。在清代與筆算、比例規演演算法等一起傳入中國,北京故宮博物院至今還藏有此算籌。 17世紀初,計算工具在西方呈現了較快的發展。首先創立對數概念 聞名於世的英國數學家納皮爾(J.Napier),在他所著的一本書里,介紹了一種新工具,即後來被稱為“納皮爾算籌”的器具。納皮爾出身在蘇格蘭一個貴族家庭,13歲就進入聖安德魯斯大學學習。作為一個天文愛好者,他曾醉心於鑽研占星術,自然而然進入到數學計算的領域。納皮爾想過許多辦法來簡化天文數值計算,終於在1614年提出了對數的概念,成為與17世紀出現的解析幾何、微積分一樣重要的數學方法,納皮爾也因此一舉成名。據說,納皮爾的這種器具發明於1612年,它由一些長條狀的木棍組成,木棍的表面雕刻著類似於乘法表的數字。納皮爾用它來幫助進行乘法計算,他根據乘數和被乘數排列好木棍的順序,僅需要做簡單的加法就能計算出乘積,從而大大簡化了數值計算過程。納皮爾算籌與中國的算籌在原理上大相徑庭,它已經顯露出對數計算方法特徵。
納皮爾開創的對數概念影響了一代數學家,英國牧師奧卻德(W.Oughtred)就是其中的佼佼者。雖然這位牧師後來爬到了主教的位置,仍然把全部業餘時間花在數學上,甚至一天只睡二三個小時。他發明的乘法符號“×”一直沿用至今。