組構
組構
組構,岩石中的各個組分以及組分之間的邊界在空間的相互排列方式,用於描述岩石中幾何性和物理性組構要素的內部幾何組態。
目錄
岩組學中,組分一詞泛指岩石的組成要素,包括組成岩石的礦物及其晶格的質點、鮞粒、礦物的集合體(如礫石)等,以及各種類型的線理、面理,也包括岩石的物理性質。在某一特定域內,岩石的組分在統計上遍及整個岩石體,其排列方式形成某種組構。在這種意義上,岩石的組成要素又稱組構要素。所有的組構要素在某一規模上可以視為構造不連續面和不連續線。組構要素有兩種類型:結晶學組構要素(礦物的晶面、晶棱、光率體主軸)和非結晶學組構要素(集合體中可見的構造不連續面和不連續線)。因此,組構是指面和線在三度空間的無限排列。組構分為幾何組構和由幾何組構所控制的物理組構。在統計上,組構具有類似於單晶體晶格構造的幾何性質、對稱性、無限延伸性、透入性以及統計均勻性。由所有組構要素的空間排列而成的組構稱為全組構。由一種組構要素而顯示的組構稱為亞組構。在特定的岩石中,亞組構能代表該岩石的組構特徵。
在岩組學中,引用單晶體點陣對稱性來描述和劃分組構的幾何特徵。組構的對稱性取決於亞組構的對稱性和組構要素自身的對稱性。在岩石亞組構中出現下列 5種對稱型(見圖):①球對稱,由組構要素的隨機定向而形成的對稱性,類似於球體所具有的對稱要素,為均質亞組構(圖a)。②軸對稱,具有圓柱體或旋轉橢球體所具有的對稱要素:一個無限次的對稱軸,並是無限多個對稱面的交線,與其垂直的面也是一個對稱面。在垂直於這個無限次對稱軸的各個方向上,亞組構相同(圖b)。③斜方對稱,具有三軸橢球體所具有的對稱要素:三個互相垂直的對稱面(ab、bc、ac)和三個與其垂直的二次對稱軸(圖c)。④單斜對稱,僅有一個對稱面(ac)和一個與其垂直的二次對稱軸(圖d)。⑤三斜對稱,沒有對稱面,只有對稱心(圖e)。這種亞組構不能藉助對稱面或對稱軸來描述。如果岩組圖的形態與上述某一種對稱型相差約10度,則在這種對稱型之前冠以“似”字,如似球對稱、似斜方對稱等。全組構的對稱性不能高於它的任何一個亞組構的對稱性。全組構的對稱型也有上述5種。
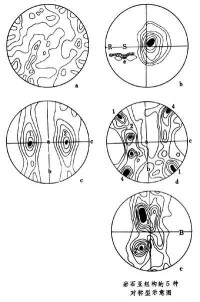
組構