普朗克公式
普朗克公式
德國物理學家M.普朗克在量子論基礎上建立的關於黑體輻射的正確公式。
19世紀末,經典統計物理學在研究黑體輻射時遇到了巨大的困難:由經典的能量均分定理導出的瑞利-金斯公式在短波方面得出同黑體輻射光譜實驗結果相違背的結論。同時,維恩公式則僅適用於黑體輻射光譜能量分佈的短波部分,也就是說,當時還未能找到一個能夠成功描述整個實驗曲線的黑體輻射公式。
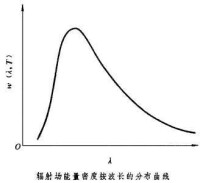
輻射場能量密度按波長的分佈曲線
式中v是振子的振動頻率,h是普朗克常數,它是量子論中最基本的常數。根據這個假設,可以導出普朗克公式:
它給出輻射場能量密度按頻率的分佈,式中T是熱力學溫度,k是玻耳茲曼常數。如圖表示輻射場能量密度隨波長變化的曲線,它同實驗結果完全一致。
作為黑體的空腔內的輻射場,既可以分解為一系列單色平面波的疊加,又可看作是由光子組成的"氣體"。光子的能量ε、動量p、波長λ和頻率v之間遵從德布羅意關係ε=hv,
則有ε=сp,在p到p+dp的動量間隔內,光子的量子態數目為
其中V是空腔的體積。只有腔壁不斷發射和吸收光子才能在輻射場中建立起熱平衡,所以光子"氣體"中的光子數就不恆定,這意味著光子"氣體"的化學勢為零。而且,光子彼此間沒有相互作用,光子"氣體"是遵從玻色分佈的理想氣體。於是,每個量子態上的平均光子數應為這樣容易得到普朗克公式。
普朗克公式在高頻範圍hvkT的極限條件下,過渡到維恩公式
此式表明,w(v,T)隨著v的增加很快地趨近於零,也就是說在熱平衡狀態下,幾乎不存在高頻光子,這是因為高頻光子的能量遠大於kT,而腔壁發射這樣高能量的光子的幾率是極小的。普朗克公式在低頻hv<量子理論就過渡到經典理論。
普朗克通過對黑體輻射的深刻研究而建立起來的公式是物理學的一個重大突破,他首次提出的量子論,開創了理論物理學發展的新紀元。

普朗克
