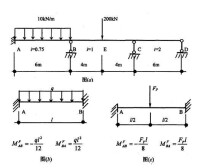
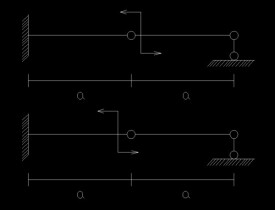
彎矩
一種力矩定理定律
彎矩是受力構件截面上的內力矩的一種。通俗的說法:彎矩是一種力矩。另一種解釋說法,就是彎曲所需要的力矩,下部受拉為正(上部受壓),上部受拉為負(下部受壓)。它的標準定義為:與橫截面垂直的分佈內力系的合力偶矩。
計算公式M=θ·EI/L,θ轉角,EI轉動剛度,L桿件的有效計算長度。
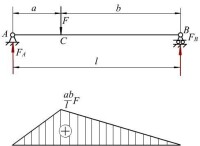
彎矩 圖3
圖4中,M就是彎矩作用,v就是剪力作用,n就是軸力作用。
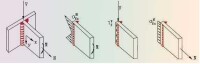
彎矩 圖4
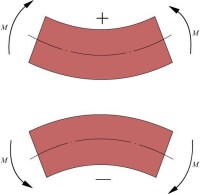
彎矩 圖1
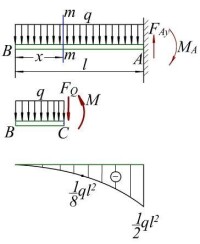
彎矩 圖2
一般而言,在不同的學科中彎矩的正負有不同的規定。規定了彎矩的正負,就可以將彎矩進行代數計算。
在列彎矩計算時,應用“左上右下為正,左下右上為負”的判別方法。凡截面左側樑上外力對截面形心之矩為順時針轉向,或截面右側外力對截面形心之矩為逆時針轉向,都將產生正的彎矩,故均取正號;反之為負,即 左順右逆,彎矩為正。
對於土木工程結構中的一根梁(指水平向的構件),當構件區段下側受拉時,我們稱此區段所受彎矩為正彎矩;當構件區段上側受拉時,我們稱此區段所受彎矩為負彎矩。
PKPM給出的彎矩方向:
作用力方向(對基礎):軸力 N 壓為正(↓);
彎矩 M 順時針為正(-↓);
剪力 V 順時針為正(→)。
彎矩公式:
表示最大彎矩,F表示外力,L即為力臂)。
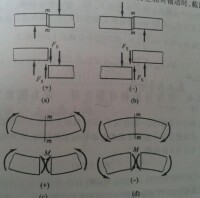
彎矩圖
(1)在梁的某一段內,若無分佈載荷作用,即,由可知,M(x)是x的一次函數,彎矩圖是斜直線。
(2)在梁的某一段內,若作用分佈載荷作用,即,則,可以得到M(x)是x的二次函數。彎矩圖是拋物線。
(3)在梁的某一截面內,若,則在這一截面上彎矩有一極值(極大或極小)。即彎矩的極值發生在剪力為零的截面上。
圖6-9 a、b、c分別畫出了同一根粱AB受q、M兩種載荷作用、q單獨作用及M單獨作用的三種受力情況。
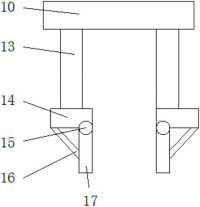
疊加原理圖
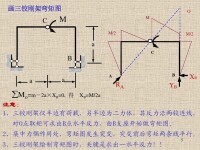
推導過程