對數正態分佈
專業術語
對數正態分佈(logarithmic normal distribution)是專業術語,拼音為duì shù zhèng tài fèn bù,指一個隨機變數的對數服從正態分佈,則該隨機變數服從對數正態分佈。對數正態分佈從短期來看,與正態分佈非常接近。但長期來看,對數正態分佈向上分佈的數值更多一些。
有些量本身就是不對稱的。例如,試想,人們完成某項特定任務需要的時間:因為每個人都是不同的,我們會得到一個分佈。然而,所有的值都必然是正數(因為時間不可能為負數)。而且,我們還能預測到該分佈可能的形狀:有一個無人可及的最小時間,然後是少數一些非常快的“冠軍”,接下來就是普通人的最具代表性的完成時間形成一個高峰,最後是尾部一長串的“掉隊者”。顯然,高斯分佈不會很好地描述這樣的分佈,因為高斯分佈中x可以定義為正值,也可定義為負值,它是對稱的且尾部很短。
在很多應用中,特別是在可靠性和維修性方面,數據可能不符合正態分佈。可是,隨機變數的對數可能符合正態分佈,對此情況稱為對數正態分佈。如果應用對數正態分佈,在對數正態圖紙上數據的圖形將是一條直線。繪圖的過程與其他分佈是相同的。其分析的過程包括計算對數值的平均值和標準差,以及對最終結果取反對數。
對數正態分佈與正態分佈很類似,除了它的概率分佈向右進行了移動。對數正態分佈從短期來看,與正態分佈非常接近。但長期來看,對數正態分佈向上分佈的數值更多一些。更準確地說,對數正態分佈中,有更大向上波動的可能,更小向下波動的可能。
已知對數正態分佈的密度函數,就可以根據可靠度與不可靠度函數的定義計算出該分佈的可靠度函數和不可靠度函數的表達式。
在概率論與統計學中,對數正態分佈是對數為正態分佈的任意隨機變數的概率分佈。如果 X 是服從正態分佈的隨機變數,則 服從對數正態分佈;同樣,如果 Y 服從對數正態分佈,則服從正態分佈。如果一個變數可以看作是許多很小獨立因子的乘積,則這個變數可以看作是對數正態分佈。一個典型的例子是股票投資的長期收益率,它可以看作是每天收益率的乘積。
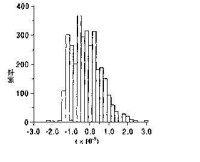
對數正態分佈
陳文華
對數正態分佈、幾何平均數與幾何標準差是相互關聯的。在這種情況下,幾何平均值等於 ,幾何
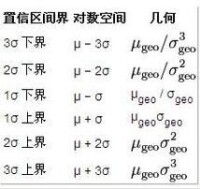
對數正態分佈
如果採樣數據來自於對數正態分佈,則幾何平均值與幾何標準差可以用於估計置信區間,就像用算術平均數與標準差估計正態分佈的置信區間一樣。
