期望效用函數理論
期望效用函數理論
期望效用函數理論(Expected Utility Theory),期望效用函數理論是20世紀50年代,馮·諾依曼和摩根斯坦(Von Neumann and Morgenstern)在公理化假設的基礎上,運用邏輯和數學工具,建立了不確定條件下對理性人(rational actor)選擇進行分析的框架。不過,該理論是將個體和群體合而為一的。後來,阿羅和德布魯(Arrow and Debreu)將其吸收進瓦爾拉斯均衡的框架中,成為處理不確定性決策問題的分析範式,進而構築起現代微觀經濟學並由此展開的包括宏觀、金融、計量等在內的宏偉而又優美的理論大廈。
如果某個隨機變數X以概率Pi取值xi,i=1,2,…,n,而某人在確定地得到xi時的效用為u(xi),那麼,該隨機變數給他的效用便是:
U(X) = E[u(X)] = P1u(x1) + P2u(x2) + ... + Pnu(xn)
其中,E[u(X)]表示關於隨機變數X的期望效用。因此U(X)稱為期望效用函數,又叫做馮·諾依曼—摩根斯坦效用函數(VNM函數)。另外,要說明的是期望效用函數失去了保序性,不具有序數性。
EU理論及SEU理論描述了“理性人”在風險條件下的決策行為。但實際上人並不是純粹的理性人,決策還受到人的複雜的心理機制的影響。因此,EU理論對人的風險決策的描述性效度一直受到懷疑。例如,EU理論難以解釋阿萊悖論、Ellsberg悖論等現象;沒有考慮現實生活中個體效用的模糊性、主觀概率的模糊性;不能解釋偏好的不一致性、非傳遞性、不可代換性、“偏好反轉現象”、觀察到的保險和賭博行為;現實生活中也有對EU理論中理性選擇上的優勢原則和無差異原則的違背;實際生活中的決策者對效用函數的估計也違背EU理論的效用函數。
另外,隨著實驗心理學的發展,預期效用理論在實驗經濟學的一系列選擇實驗中受到了一些“悖論”的挑戰。實驗經濟學在風險決策領域所進行的實驗研究最廣泛採取的是彩票選擇實驗(lottery-choice experiments),即實驗者根據一定的實驗目標,在一些配對的組合中進行選擇,這些配對的選擇通常在收益值及贏得收益值的概率方面存在關聯。通過實驗經濟學的論證,同結果效應、同比率效應、反射效應、概率性保險、孤立效應、偏好反轉等“悖論”的提出對預期效用理論形成了重大衝擊。
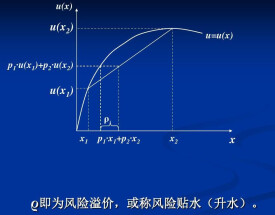
CE 被稱作確定性等值(Certainty. Equivalent),即消費者為達到期望的效用水平所要求保證的財產水平。若某人的財富效用函數為u(x),而一個賭局對某人的效用為E(u(x)),則有一個CE值能夠滿足:u(CE)=E(u(x))。稱CE為某人在該賭局中的確定性等值。
案例:期望效用函數理論在就業管理中的應用
一、就業期望效用函數的構造
從不確定性出發,考慮人們的偏好與效用函數就得引進概率P。概率的效用函數表達式叫期望效用函數,如果把期望效用函數與大學生擇業、就業結合就可以較簡單地構造出就業期望效用函數探討大學生就業的現象機制一般來講是在條件確定時進行的經驗或者理性的推導。但是,許多場合,那種以完全確定為前提的分析是不現實的。事實上,我們知道,畢業生在決策時,對於選擇的後果是不完全知道的,具有不確定性,要冒一定的風險。
畢業生的決策是取決於他(她)關於選擇某一個工作崗位的概率分佈的主觀猜測。如果他主觀認為選擇某一工作發展前景概率更高,那麼,它就會選擇,否則另謀出路。這就是我們必須從不確定性出發,考慮消費者的偏好與效用函數就得引進概率P使之變成期望效用函數。如果你選擇的工作對象是兩家IT公司,收入見下表。
表工資收入。
| 結果1 | 結果2 | |||
| 可能性(P) | 收入 | 可能性(P) | 收入 | |
| 工作A:(傭金制) | 0.6 | 2000 | 0.4 | 1000 |
| 工作B:(固定資金) | 0.95 | 1500 | 0.05 | 500 |
期望收入=(結果1的概率)×(結果1的收入)+(結果2的概率)×(結果2的收入)。工作A=1600。工作B=1450則你應該選擇工作A,而期望效用(expected utility)一般在單賭的情況下值為u(g)=pu(A)+(1-P)u(B)當u(g1) > u(g2)時,則可認為畢業時在g_1與g_2之間更偏好g_1。也就是說,當尋找工作的畢業生有多種未知的情況,而要選擇時,他們能夠依靠期望效用的極大化來代表分析自己的主觀選擇。如果選擇工作的結果有,n個可能性,即就業期望效用函數的意義在於,當大學生面臨不確定性的擇業、就業選擇時,他可以依靠期望效用的極大化來分析自己的選擇是否合理可行,至少可以對的狀況做較規範的分析。
二、效用函數應用實例
假設市場上由三份工作可以選擇,它們的工資分別為A=(3000元,1500元,1000元)括弧中的a1 = 3000,a2 = 1500,a3 = 1000,分別表示可能發生的三種結果,這裡a1最好,a3最次。
如果問自己:當a發生的概率(p)等於多少時使你認為a(i=1,2,3)與(p徠,a1,a2)無差異?如果回答是:3000元~(1×(3000元),0×(1000元),1500元~(0.6×(3000元),0.4×(1000元)),1000元~(0×(3000元),1×(1000元))那麼可以定義:
u=(3000元) =u(a1) = 1
u=(1500元) =u(a2) =O.6
u=(1000元)=u(a3) =O
可以比較不同尋職格局了。
由於 ( 1) > ( 2)即 1的期望效用大於 2的期望效用,所以你=定會偏好於選擇 1。因此就業者可以通過自己對某=行業的了解及心理自測的評價,利用就業期望效益較合理評估自己的想法,尋找更多的機會和更合適的工作崗位。
研究者針對以上問題提出了以下幾種使EU理論一般化的方式:
(1)Karmark(1978)提出主觀權重效用(Subjectively Weighted Utility,SWU)的概念,用決策權重替代線性概率,這可以解釋Allais問題和共同比率效應,但不能解釋優勢原則的違背;
(2)擴展性效用模型(generalized utility model)。該類模型的特點是針對同結果效應和同比率效應等,放鬆預期效用函數的線性特徵,或對公理化假設進行重新表述,模型將用概率三角形表示的預期效用函數線性特徵的無差異曲線,擴展成體現局部線性近似的扇行展開。這些模型沒有給出度量效用的原則,但給出了效用函數的許多限定條件。
(3)Kahneman和Tversky(1979)引入系統的非傳遞性和不連續性的概念,以解決優勢違背問題;
(4)“後悔”的概念被引入,以解釋共同比率效應和偏好的非傳遞性;如Loomes和Sudgen(1982)所提出的“後悔模型”引入了一種後悔函數,將效用奠定在個體對過去“不選擇”結果的心理體驗上(放棄選擇后出現不佳結果感到慶幸,放棄選擇后出現更佳結果感到後悔),對預期效用函數進行了改寫(仍然保持了線性特徵)。
(5)允許決策權重隨得益的等級和跡象變化,這是對SWU的進一步發展。
(6)非可加性效用模型(non-additivity utility model)這類模型主要針對埃爾斯伯格悖論,該模型認為概率在其測量上是不可加的
以上提出的幾條分別擴展為金融學中的幾大經典成果,如Kahneman和Tversky(簡稱KT)提出的理論後來發展成為前景理論;而“後悔“概念演化為“後悔理論”。