共找到2條詞條名為簡諧振動的結果 展開
- 振動形式之一
- 簡諧波
簡諧振動
振動形式之一
簡諧振動是振動的一種形式。一個作直線振動的質點,如果取其平衡位置為原點,取其運動軌道沿`x`軸,那麼當質點離開平衡位置的位移`x`隨時間`t`變化的規律,遵從餘弦函數或正弦函數時:`x=Acos(2*π*t/T+φ)`,這一直線振動便是簡諧振動。式中`A`表示質點離開平衡位置時`(x=0)`的最大位移絕對值,稱“振輻”,`T`是簡諧振動的周期,`(2*π*t/T+φ)`角稱為簡諧振動的周相角或位相。
①物體在受到大小跟位移成正比,而方向恆相反的合外力作用下的運動,叫做簡諧振動。②物體的運動參量,隨時間按正弦或餘弦規律變化的振動,叫做簡諧振動。
以x表示位移,t表示時間,這種振動的數學表達式為:
簡諧振動
簡諧振動
式中A為位移x的最大值,稱為振幅,它表示振動的強度;ωn表示每秒中的振動的幅角增量,稱為角頻率,也稱圓頻率;
稱為初相位。以f=ωn/2π表示每秒中振動的周數,稱為頻率;它的倒數,T=1/f,表示振動一周所需的時間,稱為周期。振幅A、頻率f(或角頻率ωn)、
初相位,稱為簡諧振動三要素。
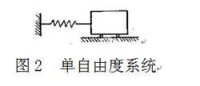
如圖2所示,由線性彈簧聯結的集中質量m構成簡諧振子。當振動位移自平衡位置算起時,其振動方程為:
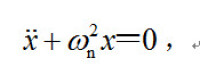
簡諧振動
簡諧振動
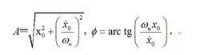
簡諧振動
但ωn只由系統本身的特徵m和k決定,與外加的初始條件無關,故ωn亦稱固有頻率。
簡諧振動
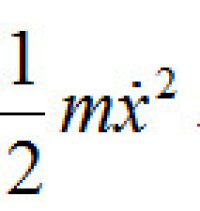
簡諧振動
簡諧振動
①振動中最簡單的就是簡諧振動。實際上,物體的運動參量隨時間按正弦或餘弦規律變化,是物體受到大小跟位移成正比,方向恆相反的合外力作用的必然結果。
②作簡諧振動的物體,回復力和位移成正比這一點,是比較容易理解的,但是對於方向恆相反這一點,初學者並不容易理解,錯誤地認為在物體由平衡位置向最大位移處運動的過程中,位移是指向最大位移處,這和所受的作用力反向;由最大位移處向平衡位置運動的過程中,位移是指向平衡位置,這和所受的作用力同向;這樣似乎外力和位移的方向時而相反,時而相同了。造成這種看法主要是由於不理解簡諧振動中,位移始終是指物體相對於平衡位置的位置變化,這就是說,物體對平衡位置的位移總是背向平衡位置。而回復力的方向總是指向平衡位置,所以二者方向恆相反。
③在教學中,我們還要強調,作簡諧振動的物體除了受到大小跟位移成正比、方向恆相反的回復力作用外,不受其他不平衡力的作用,或者說物體所受的合外力大小和位移成正比,方向恆相反。對於既受大小跟位移成正比、方向恆相反的回復力作用,同時又受其他不平衡力作用(如阻力),物體所作振動就不是一種簡諧振動。
④我們一般可以用四種方法去描述簡諧振動。
a.動力學方法。即∑F=-kx,a=-kx/m。其中t1,t2時刻位移相同,圖像運動趨勢表示其速度方向.
b.運動學方法。即x= Acos(ωt+φ),v= -Aωsin(ωt+φ),a=- Aω^2cos(ωt+φ)。
c.振動圖線法。如圖,x軸為時間,y軸為物體的位移
d.矢量圖示法,也就是參考圓法。
我們往往在分析簡諧振動時,採用參考圓法,那麼參考點以角速度ω旋轉時,它的投影就代表了給定的簡諧振動的位移規律。這時參考點的角速度跟振動的角頻率相對應。應該指出,用參考圓研究簡諧振動僅僅只是一種方法,兩種運動是不同性質的機械運動,它們之間沒有什麼必然的聯繫。
這四種方法分別從不同的角度反映了簡諧振動,在教學中不要混淆。
⑤作簡諧振動的物體振幅不變,而且物體的位移、加速度最大時,速度為零;位移、加速度為零時,速度最大。這些事實說明了物體系的勢能和動能之間不斷地相互轉換,而且物體系的總能量保持一定。因此,任何時刻物體系的總能量等於它的勢能極大值,也等於動能極大值。即任何時刻的勢能。
如何比較兩個同頻率簡諧振動的振動步調?比較兩個簡諧振動在同一時刻的相位,如果振動2與振動1的相位差大於零,則表明振動2的相位超前。
回復力的定義:振子受迫使它回復平衡位置的力,是合外力平行於速度方向上的分力。
如果用F表示物體受到的回復力,用x表示小球對於平衡位置的位移,根據胡克定律,F和x成正比,它們之間的關係可用下式來表示:
F = - kx
式中的k是回復力與位移成正比的比例係數,不能與彈簧的勁度係數混淆;負號的意思是:回復力的方向總跟物體位移的方向相反。
一般簡諧運動周期:T=2π√(m/k). 其中m為振子質量,k為振動系統的回復力係數。
對於單擺運動,其周期T=2π√(L/g) (π為圓周率 √為根號)由此可推出g=(4π^2×L)/(T^2) 據此可利用實驗求某地的重力加速度。
T與振幅(a<10度)和擺球質量無關。
當偏角a<10度時 sina≈a=弧(軌跡)/L(半徑)≈x/L;F回=-mg/Lx
根據牛頓第二定律,F=ma,運動物體的加速度總跟物體所受的合力的大小成正比,並且跟合力的方向相同。
振幅、周期和頻率
簡諧運動的頻率(或周期)跟振幅沒有關係。
物體的振動頻率本身的性質決定,所以又叫固有頻率。
一個做勻速圓周運動的物體在一條直徑上的投影所做的運動即為簡諧振動:R是勻速圓周運動的半徑,也是簡諧振動的振幅;ω是勻速圓周運動的角速度,也叫做簡諧振動的圓頻率,ω=√(k/m);φ是t=0時勻速圓周運動的物體偏離該直徑的角度(逆時針為正方向),叫做簡諧振動的初相位。在t時刻,簡諧振動的位移x=Rcos(ωt+φ),簡諧振動的速度v=-ωRsin(ωt+φ),簡諧振動的加速度a=-(ω^2)Rcos(ωt+φ)=-ω^2*x,這三個式子叫做簡諧振動的方程。
這個運動是假設在沒有 能量損失引至阻力的情況而發生。
做簡諧振動的物體的加速度跟物體偏離平衡位置的位移大小成正比,方向與位移的方向相反,總指向平衡位置.
一個做勻速圓周運動的物體在一條直徑上的投影所做的運動即為簡諧運動:R是勻速圓周運動的半徑,也是簡諧運動的振幅;ω是勻速圓周運動的角速度,也叫做簡諧運動的圓頻率,ω=√(k/m);φ是t=0時勻速圓周運動的物體偏離該直徑的角度(逆時針為正方向),叫做簡諧運動的初相位。在t時刻,簡諧運動的位移x=Rcos(ωt+φ),簡諧運動的速度v=-ωRsin(ωt+φ),簡諧運動的加速度a=-(ω^2)Rcos(ωt+φ),這三個式子叫做簡諧運動的方程。
這個運動是假設在沒有能量損失引至阻力的情況而發生。
做簡諧運動的物體的加速度跟物體偏離平衡位置的位移大小成正比,方向與位移的方向相反,總指向平衡位置。
方程:(d x)*(d x)/(d t*t)+kx/m=0
通解:x(t)=c1*cos(kt)+c2*sin(kt)
特解:x(t)=x0*cos(kt)+v0/k*sin(kt)
令:x0=Asinθ結論:Asin(kt+θ)
振幅為A,初相為θ,周期為T=2π/k,角頻率為k。
其中k為系統的固有頻率。
當物體到最低點時,v=f(x)取極值,速率取最大值,此時a=f'(x)=0。
當物體到最高點時,v=f(x)=0,速率取最大值,此時a=f'(x)在不同方向上最大。
在阻力作用下的簡諧運動。
簡諧運動
振動過程中受到阻力的振動,振幅逐漸減小,直至振動停止。
振動方程:x=Ae^(-nt)sin(wt+θ).
在外界驅動力作用下的簡諧振動,頻率只與驅動力頻率有關。
驅動力頻率越接近固有頻率,振幅越大。
驅動力頻率與固有頻率相等時,振幅隨時間正比增大,發生共振。
受迫振動與共振:
⑴受迫振動:振動系統在周期性策動力作用下的振動。穩定時,系統的振動頻率等於策動力的頻率,跟系統的固有頻率無關。
⑵共振:當策動力的頻率等於系統的固有頻率時振幅最大稱為共振。
