等角半正多面體
等角半正多面體
等角半正多面體(equiangular semiregular polyhedron)亦稱阿基米德多面體,是一種特殊的多面體,指所有多面角都相等,且各個面是邊數不全相同的正多邊形的多面體,等角半正多面體的多面角最多有五個面,側面是正方形的正n稜柱是等角半正(n+2)面體,又如取正n面體(n=6或8,12或20)各棱的中點作為頂點所成的多面體也是等角半正多面體,分別稱為立方八面體或中央晶體(由六個正方形和八個正三角形圍成的)和十二兼二十面體(由十二個正五邊形和二十個正三角形圍成的) 。
如果多面體的面是由幾種不同的正多邊形組成,而它們的多面角都相等,這樣的多面體叫做 等角半正多面體。如果多面體的多面角是幾種不同的角度而各面都相等,這種多面體就叫做等面半正多面體。
三維空間中共有十三種等角半正多面體(見表1)。半正多面體是由正多面體演變得來的。
| 表1 十三種等角半正多面體 | ||
|---|---|---|
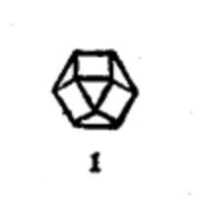 等角半正多面體 | 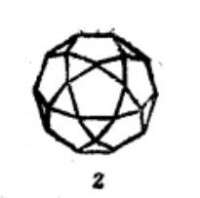 等角半正多面體 | 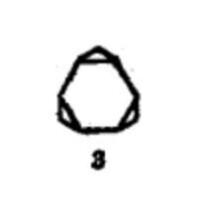 等角半正多面體 |
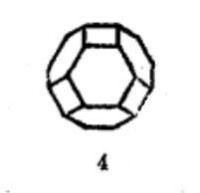 等角半正多面體 | 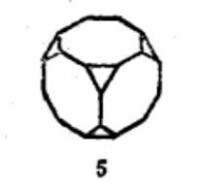 等角半正多面體 | 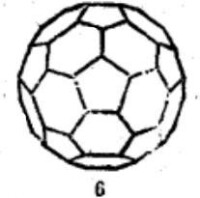 等角半正多面體 |
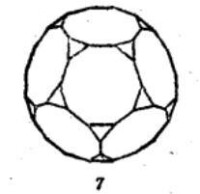 等角半正多面體 | 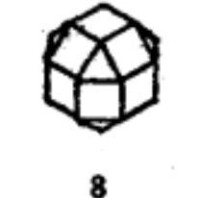 等角半正多面體 | 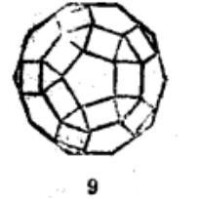 等角半正多面體 |
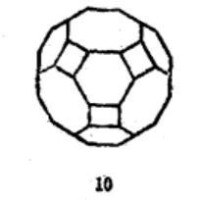 等角半正多面體 | 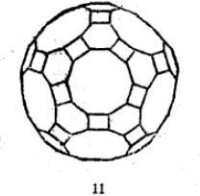 等角半正多面體 | 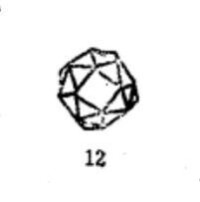 等角半正多面體 |
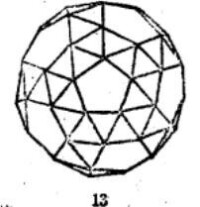 等角半正多面體 | ||
如果把正四面體的各棱中點同一組線連接起來,就可以發現這組線構成了一個正八面體。同法,把六面體或八面體的各棱中點連線,結果是一個立方八面體,把十二面體或者二十面體的各棱中點連線,結果叫做十二兼二十面體(見圖1)。由此可知,正多面體各棱中點連線可生成八面體、立方八面體和十二兼二十面體。正是由於中點將各棱分成兩段,因此又稱這三種形體為二次形體。
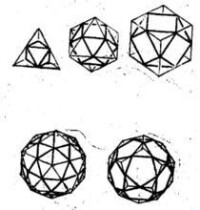
圖1 二次形體
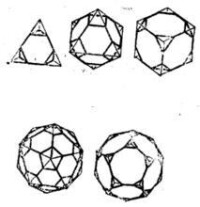
圖2 三次形體
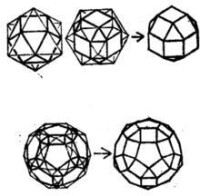
圖3 四次形體
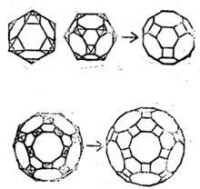
圖4 六次形體
等角半正多面體的一些特徵:
1.形體上每個多面角相等
半正多面體的面和正多面體一樣,是由正多邊形組成,不同的是正多面體的所有面是同一種類型的正多邊形,而半正多面體卻是兩種或兩種以上類型的正多邊形面。由於各種形體在每一頂點處的面是同樣規律排列的,所以它的每一頂點處的面角和必定是一樣的。
正多面體上相鄰兩面間的二面角是不變數,半正多面體中除了立方八面體和十二兼二十面體的二面角也都是不變數外,其它形體則有兩種或三種不同的二面角。舉例來說,從一個截頂六面體的模型來看,其兩個相鄰的八邊形的二面角是90°,而八邊形與其相鄰的三角形間的二面角雖然是不變數,但很明顯它不是90°,實際上是125°16'。
2.半正多面體都有一個外接球和一個內接球
由於每個半正多面體可以外切於一個正多面體,因此它的所有頂點都均勻地位於其外切形體的棱或面上,例如一個立方八面體和一個大的正交立方八面體外切於一個六面體。見圖5(a)和(b)。在每種情況中,內接形體的頂點和外切形體內的中心距離是相等的,因為從形體中心到每個正多阿體的面的中心是一個固定的距離,由形體的中心到內接形體的頂點也是一個固定的距離,因此半正多面體和正多面體一樣,具有一個外接球,它的所有頂點與其相接觸。再次,由於半正多而體的所有棱長相等,對它的外接球來說也是具有相等的弦長,從外接球中心到弦的中點距離相等,因此半正多面體像正多面體一樣有一個內接球與所有棱相接觸。但是,由於半正多面體的頂點或棱到不同類型的面的中心距離不是一個定值,從截頂八面體的六邊形或正方形即可看出[圖5中的(c)],所以,和正多面體不同,半正多面體不能作一個內球與各面相接觸。
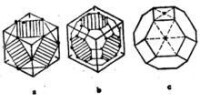
圖5
在正多面體的一些特徵中已經說明,由平面構成的任何一個凸多面體面角的總和永遠是360°×頂點數-720°,用此公式去檢驗一個半正多面體也是一一樣的。
例如,立方八面體有十二個頂點,按照公式它的面角總和等於,即3600°。這個形體有八個三角形面,每一個面的內角總和是180°,八個三角形的面角總數是1440°,它的六個正方形面,每個面的面內角和是360°,六個正方形面的內角總和是2160°,從而三角形和正方形兩項面角的總和是。這個公式對任何一個半正多面體都是適用的。
4.每個半正多面體可以外切於一個四面體
等角半正多面體的一個重要特性是可以外切於一個四面體,因此,它有四個面重合在那個四面體的各面上。舉例來說,如圖6所示,一個截頂八面體的四個六邊形面能重疊在四面體的各面。因此,半正多面體的定義是一個凸多面體,它的每個頂點周圍有兩種或兩種以上類型的正多邊形,並且它能外接於一個正四面休,它有四個面落在四面體的面上,這樣的定義就概括了十三種等角半正多面體。
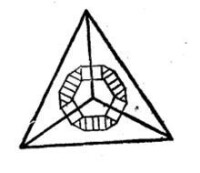
圖6