組合邏輯電路
組合邏輯電路
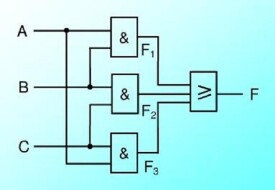
組合邏輯電路,數字電路根據邏輯功能的不同特點,可以分成兩大類,一類叫組合邏輯電路(簡稱組合電路),另一類叫做時序邏輯電路(簡稱時序電路)。組合邏輯電路在邏輯功能上的特點是任意時刻的輸出僅僅取決於該時刻的輸入,與電路原來的狀態無關。所謂邏輯問題的描述,就是將文字描述的設計要求抽象為一個邏輯表達式。通常的方法是:先建立輸入輸出邏輯變數的真值表,再由真值表寫出邏輯表達式。有些情況下,可由設計要求直接建立邏輯表達式。數字電路分為組合邏輯電路和時序邏輯電路兩類,組合邏輯電路的特點是輸出信號只是該時的輸入信號的函數,與別時刻的輸入狀態無關,它是無記憶功能的。
組合邏輯電路是指在任何時刻,輸出狀態只決定於同一時刻各輸入狀態的組合,而與電路以前狀態無關,而與其他時間的狀態無關。其邏輯函數如下:
Li=f(A1,A2,A3…….An) (i=1,2,3….m)
其中,A1~An為輸入變數,Li為輸出變數。
組合邏輯電路的特點歸納如下:
① 輸入、輸出之間沒有返饋延遲通道。
② 電路中無記憶單元。
對於第一個邏輯表達工式或邏輯電路,其真值表可以是惟一的,但其對應的邏輯電路或邏輯表達式可能有多種實現形式,所以,一個特定的邏輯問題,其對應的真值表是惟一的,但實現它的邏輯電路是多種多樣的。在實際設計工作中,如果由於某些原因無法獲得某些門電路,可以通過變換邏輯表達式變電路,從而能使用其他器件來代替該器件。同時,為了使邏輯電路的設計更簡潔,通過各方法對邏輯表達式進行化簡是必要的。組合電路可用一組邏輯表達式來描述。設計組合電路直就是實現邏輯表達式。要求在滿足邏輯功能和技術要求基礎上,力求使電路簡單、經濟、可靠、實現組合邏輯函數的途徑是多種多樣的,可採用基本門電路,也可採用中、大規模集成電路。其一般設計步驟為:
① 分析設計要求,列真值表:
② 進行邏輯和必要變換。得出所需要的羅最簡邏輯表達式;
③ 畫邏輯圖。
組合邏輯電路
在asic設計和pld設計中組合邏輯電路設計的最簡化是很重要的,在設計時常要求用最少的邏輯門或導線實現。在asic設計和pld設計中需要處理大量的約束項,值為1或0的項卻是有限的,提出組合邏輯電路設計的一種新方法。
組合邏輯電路
(1):有給定的邏輯電路圖,寫出輸出端的邏輯表達式;
(2):列出真值表;
(3):通過真值表概括出邏輯功能,看原電路是不是最理想,若不是,則對其進行改進;例1:已知邏輯電路圖,試分析其功能。
第一步:寫邏輯表達式。由前級到后級寫出各門邏輯表達式。
P=A+B S=A+P=AB W=B+P=AB
F=S+W=AB+A B
第二步:列真值表。
第三步:邏輯功能描述並改進設計。
從真值表中可以看出這是一個二變數“同或”電路。原電路設計不合理,它只需一個"同或"門即可。
半加器和全加器
在數字系統中算術運算都是利用加法進行的,因此加法器是數字系統中最基本的運算單元。由於二進位運算可以用邏輯運算來表示,因此可以用邏輯設計的方法來設計運算電路。加法在數字系統中分為全加和半加,所以加法器也分為全加器和半加器。
(1)半加器設計
半加器不考慮低位向本位的進位,因此它有兩個輸入端和兩個輸出端。
設加數(輸入端)為A、B ;和為S ;向高位的進位為Ci+1。
函數的邏輯表達式為: S=AB+AB ; Ci+1=AB
(2)全加器的設計(它的邏輯符號為圖(3)所示)
由於全加器考慮低位向高位的進位,所以它有三個輸入端和兩個輸出端。
設輸入變數為(加數)A、B、 Ci-1,輸出變數為 S、 Ci+1
函數的邏輯表達式為:S=ABCi-1+ABCi-1+ABCi-1+ABCi-1=ABCi-1
Ci+1=ABCi-1+ABCi-1+ABCi-1+ABCi-1 =(AB)Ci-1+AB
(3)全加器的應用
因為加法器是數字系統中最基本的邏輯器件,所以它的應用很廣。它可用於二進位的減法運算、乘法運算,BCD碼的加、減法,碼組變換,數碼比較等。
例 1:用全加器構成二進位減法器。
以四位二進位為例。(減法可轉換為加補運算)
設兩組四位二進位分別為X3X2X1X0和Y3Y2Y1Y0,把Y3Y2Y1Y0先進行求補然後再進行加法運算。
因為求補是逐位求反后再加“1”。
例 2:採用四位全加器完成8421BCD碼轉換為餘3代碼。
由於8421BCD碼加0011即為餘3代碼,因此轉換電路就是加法電路。
設8421BCD碼四位又高位到低位為M3、M2、M1、M0,餘3代碼的四位由高到低為C3、C2、C1、C0 。
指定二進位代碼代表特定的信號的過程就叫編碼。把某一組二進位代碼的特定含義譯出的過程叫解碼。
(1)編碼器 因為n位二進位數碼有2n種狀態,所以它可代表2n組信息。人們在編碼過程中一般是採用編碼矩陣和編碼表,編碼矩陣就是在卡諾圖上指定每一方格代表某一自然數,把這些自然數填入相應的方格。
組合邏輯電路
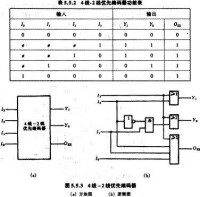
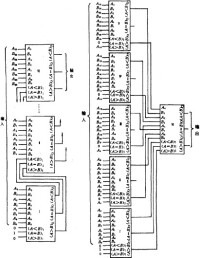
由編碼表確定各輸出端的邏輯表達式是:
A=5+6+7+8+9
B=4+9
C=2+3+7+8
D=1+3+6+8
根據這些表達式可用或門組成(2):解碼器 編碼的逆過程就是解碼。解碼就是把代碼譯為一定的輸出信號,以表示它的原意。實現解碼的電路就是解碼器。解碼器可分為二進位解碼器、十進位解碼器、集成解碼器和數字顯示解碼驅動電路。其中二進位解碼器是一種最簡單的變數解碼器,它的輸出端全是最小項。
例 2:設計一解碼電路把8421BCD碼的0、1、2、...、9譯出來.
四位二進位有十六種狀態,而實際只需要十種,因此其餘項作無關項考慮.
人們通過編碼矩陣可得如下解碼關係:
所以它的邏輯電路圖為(用與門和與非門實現)集成解碼器的工作原理與其它解碼器一樣,但它有它的特點。
它的特點為:
輸入採用緩衝級;(減輕信號負載)
輸出為反碼;低電平有效(減輕輸出功率)
增加了使能端.(便於擴展功能)
常用的典型的集成解碼器是三------八解碼器。
它的邏輯符號註:其中E0E1E2為使能端,只有當E1、E2為0時E0為1時此解碼器才工作。
數據選擇器 它就是從多個輸入端中選擇一路輸出,它相當於一個多路開關它的邏輯符號如圖(1)所示:其中D0D1、、、Dn是數據輸入端;A0A1、、、An為地址變數(有n個地址變數就有2n個輸入端).
常用的有二選一,四選一,八選一和十六選一,若需更多則由上述擴展。
例 3:四選一數據選擇器,寫出它的輸出邏輯表達式和功能表
它的邏輯輸出表達式為 F=(A0A1D0+A0A1D1+A0A1D2+A0A1D3)E
可以看出當使能端E為“1”時輸出為“0”即禁止,只有當使能端為“0”時選擇器才有效。
組合邏輯電路
八選一要有八個輸入變數,因此需要三個地址變數(把其中一個A0作為使能段);
四選一隻能有四個輸入變數,所以人們需要兩個四選一和一個非門。非門的作用是改變使能端的電平,減少使能端。
A0 A1 A2 D F
0 0 0 D0----D7 D0
0 0 1 D0----D7 D1
0 1 0 D0----D7 D2
0 1 1 D0----D7 D3
1 0 0 D0----D7 D4
1 0 1 D0----D7 D5
1 1 0 D0----D7 D6
1 1 1 D0----D7 D7
多路分配器的功能是把輸入數據分配給不同的通道上,相當於一個單刀多擲開關。