遞歸可枚舉集
遞歸可枚舉集
又稱部分遞歸集。在能行性理論中,基本概念是遞歸函數,它可刻畫為:任給x,只要它在x處有定義必可在有限步驟內求出其值。因此遞歸全函數(即處處有定義的)必可在有限步驟內求出它的任一值,至於遞歸部分函數(未必處處有定義的)則只要求有定義處可求出其值,但不要求能夠在有限步驟內判定它的定義域的元素,即對任給的x判定x是否屬於函數的定義域。
設有一集合 A與一函數α(x),如果α(x)=0當且僅當x∈A,則α(x)叫做A的特徵部分函數,如果還有α(x)=1,當且僅當x唘A,則α(x)叫做A的特徵全函數,簡稱特徵函數。如果一集合 A的特徵部分函數(也是特徵函數)是遞歸全函數,則A叫做遞歸集;如果一集A的特徵部分函數是遞歸部分函數,則A叫做部分遞歸集;部分遞歸集又可定義為某個遞歸部分函數的定義域。顯然,A為遞歸集當且僅當:任給x,x屬於A與否,恆可在有限步內判定;A為部分遞歸集當且僅當:任給x,如果x∈A,則必可在有限步內判定,但如果x唘A,可能永遠不知道這件事(除非從別的途徑)。因此有下列結果:
①如果A為遞歸集,則A為部分遞歸集;
②A為遞歸集當且僅當A的補集亦為遞歸集;
③A為遞歸集當且僅當A與它的補集都是部分遞歸集。
最後一點可看出:如果x∈A,因A為部分遞歸集必可在有限步內看出;如果x唘A,因A的補集為部分遞歸集亦可在有限步內看出,從而A必為遞歸集。
遞歸可枚舉集是指它是某個一般遞歸函數(即遞歸全函數)ƒ(x)的值域。因為遞歸全函數ƒ(x)的每一個值都可在有限步內算出,可以逐步地計算ƒ(0),ƒ(1),ƒ(2),…,從而得出遞歸可枚舉集的所有元素。這便是遞歸可枚舉集名稱的來源。ƒ(x)叫做該集的枚舉函數,可能有兩值ƒ(α)與ƒ(b)是相等的,即容許重複枚舉。如果ƒ(x)是不減函數或(嚴格)遞增函數,便叫做不減枚舉或(嚴格)遞增枚舉。
顯然,如果x在一個遞歸可枚舉集A內,必可在有限步內判定(只須依次計算ƒ(0),ƒ(1),…,便可);但如果x不在A內,而A又不是嚴格遞增枚舉,則很可能人們永遠也不知道這事。根據上述部分遞歸集的特性,可知遞歸可枚舉集都是部分遞歸集。反之,如果A為部分遞歸集,命其特徵部分函數為α(x),當A為空集時,它當然不是任何遞歸全函數的值域,當A非空集時,則在第一階段對α(0),α(1)各計算1步,第二階段對α(0),α(1),α(2)各計算2步,…,第n階段對α(0),α(1),α(2),…,α(n)各計算n步,…,並把首先出現的α(x)=0的根取為ƒ(0),以後在每一階段之末均把在該階段時所已知的α(x)=0的根取為ƒ在新主目處的值,ƒ必為遞歸全函數,而且A的元素恰巧便是ƒ(0),ƒ(1),…的值。可見非空的部分遞歸集必是遞歸可枚舉集。一般還把空集也算作遞歸可枚舉集,這樣兩種集便一致起來了。
可以證明,A為遞歸可枚舉集當且僅當它是某個原始遞歸函數的值域,又當且僅當它是某個初等函數的值域。另一方面,A為遞歸可枚舉當且僅當它是某個遞歸部分函數的值域,只須仿照上法,在第n階段計算ƒ(0),ƒ(1),…,ƒ(n)各n步,便可把遞歸部分函數的值全部都枚舉出來了。
已有辦法把全體遞歸部分函數全部枚舉起來,因此也可以把它們的定義域或值域全部枚舉起來。設把第x個遞歸部分函數的定義域(值域)記為Wx,則Wx便是全體部分遞歸集(遞歸可枚舉集)的枚舉(注意其中是有重複的)。如命K={x:x∈Wx}(即如果x恰巧在第x個部分遞歸集之內,便把x作為K 的元素),則K是一個遞歸可枚舉集但不是遞歸集,從而K 的補集既不是遞歸集又不是遞歸可枚舉集。這是人們作出的第一個不是遞歸可枚舉集的例子,它也是一個很重要的集,對它已有充分的研究。
此外,如果ƒ 為遞歸部分函數,A為遞歸可枚舉,則ƒ-1(A)也是遞歸可枚舉集。
著名的希爾伯特第10問題是:有沒有一個能行方法,可決定任給的一個不定方程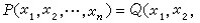
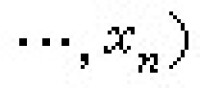 是否有整數解?這裡P、Q是兩個具有整係數的多項式。這個問題到1970年已經被否定地解決了,即如果把“能行方法”理解為“用計算遞歸全函數的方法”,那末可以證明:這個能行方法是沒有的。因為任何一個部分遞歸集(遞歸可枚舉集)A,都有兩個帶整係數的多項式P、Q,使得
是否有整數解?這裡P、Q是兩個具有整係數的多項式。這個問題到1970年已經被否定地解決了,即如果把“能行方法”理解為“用計算遞歸全函數的方法”,那末可以證明:這個能行方法是沒有的。因為任何一個部分遞歸集(遞歸可枚舉集)A,都有兩個帶整係數的多項式P、Q,使得
遞歸可枚舉集
遞歸可枚舉集
遞歸可枚舉集
遞歸可枚舉集
遞歸可枚舉集
上面關於集合的討論可以推廣到n元關係去。就n元關係R(x1,x2,…,xn)而言,如果R(x1,x2,…,xn)成立當且僅當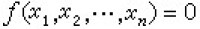 ,則ƒ(x1,x2,…,xn)叫做R(x1,x2,…,xn) 的特徵部分函數,如果還要求:R(x1,x2,…,xn)不成立當且僅當
,則ƒ(x1,x2,…,xn)叫做R(x1,x2,…,xn) 的特徵部分函數,如果還要求:R(x1,x2,…,xn)不成立當且僅當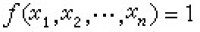 ,則ƒ 叫做R的特徵全函數,簡稱特徵函數。如果關係R(x1,x2,…,xn)的特徵部分函數(也是特徵函數)是一個遞歸全函數,則R叫做遞歸關係;如果R(x1,x2,…,xn)的特徵部分函數是遞歸部分函數,則R叫做部分遞歸關係。有了這些定義以後,以上的討論完全可以推廣到遞歸關係與部分遞歸關係方面來。當然,由於函數的值是一個數而不是n元向量,所以“遞歸可枚舉關係”不能定義為某個遞歸全函數的值域而只能定義為部分遞歸關係。
,則ƒ 叫做R的特徵全函數,簡稱特徵函數。如果關係R(x1,x2,…,xn)的特徵部分函數(也是特徵函數)是一個遞歸全函數,則R叫做遞歸關係;如果R(x1,x2,…,xn)的特徵部分函數是遞歸部分函數,則R叫做部分遞歸關係。有了這些定義以後,以上的討論完全可以推廣到遞歸關係與部分遞歸關係方面來。當然,由於函數的值是一個數而不是n元向量,所以“遞歸可枚舉關係”不能定義為某個遞歸全函數的值域而只能定義為部分遞歸關係。
遞歸可枚舉集
遞歸可枚舉集
但是對遞歸關係而論,有下列的結果,這是討論遞歸時所沒有的。
①R(x1,x2,…,xn)為部分遞歸關係當且僅當有一個n+1元遞歸關係或部分遞歸關係 W 使得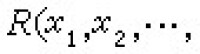
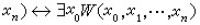 。
。
遞歸可枚舉集
遞歸可枚舉集
②R(x1,x2,…,xn)為部分遞歸關係當且僅當有一個n+m 元遞歸或部分遞歸關係W 使得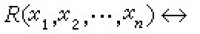
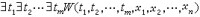 。
。
遞歸可枚舉集
遞歸可枚舉集
③A為部分遞歸集當且僅當有一個二元遞歸或部分遞歸關係W 使得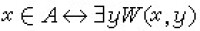 。
。
遞歸可枚舉集
可以與正整數集建立一一對應的無窮集合.
可數集合S被稱為遞歸可枚舉的, 如果存在生成S的元素的演演算法. 等價定義:可數集合S被稱為遞歸可枚舉的, 如果有一個圖靈機, 在給定S的一個元素作為輸入的時候總是停機, 並在給定的輸入不屬於S的時候永不停機.
可數集合S被稱為遞歸的, 如果存在能夠在有限步驟內判定任意給定元素是否屬於S的演演算法.
從定義中可以推導出幾個有用的性質. 所有遞歸集合都是遞歸可枚舉的, 但不是所有遞歸可枚舉集合都是遞歸的. 如果一個集合本身及其補集都是遞歸可枚舉的, 那麼這個集合是遞歸的. 顯然, 遞歸集的補集也是遞歸集.
通常的形式系統中, 所有公理構成的集合可以是有限集合, 也可以是無窮集合, 但公理集都是遞歸集. 在一階邏輯中, 所有定理構成的集合P是遞歸可枚舉集合: 存在一個可以枚舉出所有定理的演演算法. 對於只有有限條公理的情況, 這個演演算法的大致思路是: 從公理出發,將形式系統中的所有推理規則依次作用於每一條公理得到第一批定理, 再將所有推理規則依次作用於第一批定理得到第二批定理, 照此不斷進行下去. 於是我們看到, 每一個形式系統中的P都是遞歸可枚舉集合.
皇帝新腦中指出P不是遞歸的, 也就是說一般地說不存在一個能夠依次生成P的補集中的元素的演演算法. 我的理解是, 可以構造一個簡單的形式系統(比如集異璧中的“pq系統”)使其中所有定理構成的集合P是遞歸的, 不過也存在一些形式系統, 其集合P是非遞歸的. 事實上這一結論並不是顯然的, 因為它與哥德爾定理具有相同的深度. 通常的想法是, 形式系統中所有命題要麼能被證明要麼能被證偽. 注意任一可證偽的命題恰好是P中某一個命題的逆命題, 所以所有可證偽的命題構成的集合是遞歸可枚舉的. 如果P不是遞歸的, 也就是說, P的補集不是遞歸可枚舉的, 那麼P的補集中除了可證偽的命題之外一定還包括既不可證明又不可證偽的命題. 因為在滿足哥德爾定理條件的“足夠強”的形式系統中存在著既不可證明又不可證偽的命題, 所以對於形式系統, P是非遞歸的遞歸可枚舉集.