納維-斯托克斯方程
1827年納維首先提出的方程式
納維-斯托克斯方程是牛頓第二定律在不可壓縮粘性流動量守恆的運動方程,簡稱N-S方程。
粘性流體的運動方程首先由納維在1827年提出,只考慮了不可壓縮流體的流動。泊松在1831年提出可壓縮流體的運動方程。聖維南與斯托克斯在1845年獨立提出粘性係數為一常數的形式,都稱為Navier-Stokes方程,簡稱N-S方程。三維空間中的N-S方程組光滑解的存在性問題被美國克雷數學研究所設定為七個千禧年大獎難題之一。
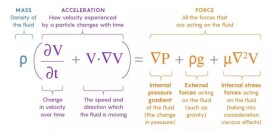
牛頓第二定律在不可壓縮粘性流動中的表達式。簡稱N-S方程。此方程是法國力學家、工程師C.-L.-M.-H.納維於1821年創立,經英國物理學家G.G.斯托克斯於1845年改進而確定的。它的矢量形式為:
在直角坐標中的分量形式為:
納維-斯托克斯方程
納維-斯托克斯方程
納維-斯托克斯方程
式中ρ、ν、p、u、f分別為液體密度、運動粘性係數、動水壓強、流速矢量、單位質量的質量力;墷為矢量微分算符;為拉普拉斯算符。為指定點處由於時間改變而引起的速度變化率,稱為當地加速度;(u·墷)u 為指定瞬時由於空間位置改變而引起的速度變化率,稱為遷移加速度;與ν墷2u分別為作用於單位質量液體表面的合壓力與合粘性力;及為u及f在直角坐標中的投影。
在某些情況下,合粘性力很小,可忽略不計,於是N-S方程簡化為理想液體的歐拉方程。即:
對於需作流場分析的水力學問題,N-S方程有特別重要的意義。它和三維連續性方程一道組成不可壓縮粘性流動完整方程組,附加一定的初始條件和邊界條件,從理論上講,就可以解出流速分佈和壓強分佈。但N-S方程是非線性的二階偏微分方程,僅在一些特定條件下,才能求出解析結果。對於低雷諾數流動,可全部地或部分地略去慣性項,求得蠕動流近似解。對高雷諾數流動,在物體表面附近的邊界層內,必須考慮粘性影響,按邊界層方程求解;邊界層外,粘性效應可以忽略,用歐拉方程近似求解。在很多情況下,特別是中等雷諾數的流動,可求出N-S方程的數值解。大型電子計算機的應用,為N-S方程的數值解開闢了廣闊的前景。
後人在此基礎上又導出適用於可壓縮流體的N-S方程。以應力表示的運動方程,需補充方程才能求解。N-S方程反映了粘性流體(又稱真實流體)流動的基本力學規律,在流體力學中有十分重要的意義。它是一個非線性偏微分方程,求解非常困難和複雜,在求解思路或技術沒有進一步發展和突破前只有在某些十分簡單的特例流動問題上才能求得其精確解;但在部分情況下,可以簡化方程而得到近似解。例如當雷諾數 時,繞流物體邊界層外,粘性力遠小於慣性力,方程中粘性項可以忽略,N-S方程簡化為理想流動中的歐拉方程;而在邊界層內,N-S方程又可簡化為邊界層方程,等等。在計算機問世和迅速發展以來,N-S方程的數值求解才有了較大的發展。
從理論上講,有了包括N-S方程在內的基本方程組,再加上一定的初始條件和邊界條件,就可以確定流體的流動。但是,由於N-S方程比歐拉方程多了一個二階導數項,因此,除在一些特定條件下,很難求出方程的精確解。
可求得精確解的最簡單情況是平行流動。這方面有代表性的流動是圓管內的哈根-泊肅葉流動(詳見管流)和兩平行平板間的庫埃特流動(詳見牛頓流體)。
在許多情況下,不用解出N-S方程,只要對N-S方程各項作量級分析,就可以確定方程的特性,或獲得方程的近似解。
對於雷諾數 的情況,方程左端的加速度項與粘性項相比可忽略,從而可求得斯托克斯流動的近似解。RA·密立根【羅伯特·安德魯·密立根】根據這個解給出了一個有名的應用(密立根油滴實驗),即空氣中細小球狀油滴的緩慢流動。
對於雷諾數 的情況,粘性項與加速度項相比可忽略,這時粘性效應僅局限於物體表面附近的邊界層內,而在邊界層之外,流體的行為實質上同無粘性流體一樣,所以其流場可用歐拉方程求解。
把N-S方程沿流線積分可得到粘性流體的伯努利方程式中為重力加速度;為單位質量流體克服阻力作功而引起的機械能損失。因此,流體沿流線流動時,機械能化成熱能,使流體溫度升高。
在解釋納維-斯托克斯方程的細節之前,首先,必須對流體作幾個假設。第一個是流體是連續的。這強調它不包含形成內部的空隙,例如,溶解的氣體氣泡,而且它不包含霧狀粒子的聚合。另一個必要的假設是所有涉及到的場合,全部是可微的,例如壓強,速度,密度,溫度,等等。該方程從質量,動量守恆,和能量守恆的基本原理導出。對此,有時必須考慮一個有限的任意體積,稱為控制體積,在其上這些原理很容易應用。該有限體積記為,而表面積記為。該控制體積可以在空間中固定,也可能隨著流體運動。