人工神經網路

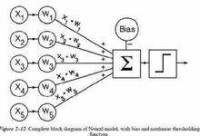
如圖所示

a1~an為輸入向量的各個分量

w1~wn為神經元各個突觸的權值

b為偏置

f為傳遞函數，通常為非線性函數。以下默認為hardlim()

t為神經元輸出

數學表示 t=f(WA'+b)

W為權向量

A為輸入向量，A'為A向量的轉置

b為偏置

f為傳遞函數

可見，一個神經元的功能是求得輸入向量與權向量的內積后，經一個非線性傳遞函數得到一個標量結果。

單個神經元的作用：把一個n維向量空間用一個超平面分割成兩部分（稱之為判斷邊界），給定一個輸入向量，神經元可以判斷出這個向量位於超平面的哪一邊。

該超平面的方程: Wp+b=0

W權向量

b偏置

p超平面上的向量

人工神經網路是由大量處理單元互聯組成的非線性、自適應信息處理系統。它是在現代神經科學研究成果的基礎上提出的，試圖通過模擬大腦神經網路處理、記憶信息的方式進行信息處理。人工神經網路具有四個基本特徵：

（1）非線性 非線性關係是自然界的普遍特性。大腦的智慧就是一種非線性現象。人工神經元處於激活或抑制二種不同的狀態，這種行為在數學上表現為一種非線性關係。具有閾值的神經元構成的網路具有更好的性能，可以提高容錯性和存儲容量。

（2）非局限性 一個神經網路通常由多個神經元廣泛連接而成。一個系統的整體行為不僅取決於單個神經元的特徵，而且可能主要由單元之間的相互作用、相互連接所決定。通過單元之間的大量連接模擬大腦的非局限性。聯想記憶是非局限性的典型例子。

（3）非常定性 人工神經網路具有自適應、自組織、自學習能力。神經網路不但處理的信息可以有各種變化，而且在處理信息的同時，非線性動力系統本身也在不斷變化。經常採用迭代過程描寫動力系統的演化過程。

（4）非凸性 一個系統的演化方向，在一定條件下將取決於某個特定的狀態函數。例如能量函數，它的極值相應於系統比較穩定的狀態。非凸性是指這種函數有多個極值，故系統具有多個較穩定的平衡態，這將導致系統演化的多樣性。

人工神經網路中，神經元處理單元可表示不同的對象，例如特徵、字母、概念，或者一些有意義的抽象模式。網路中處理單元的類型分為三類：輸入單元、輸出單元和隱單元。輸入單元接受外部世界的信號與數據；輸出單元實現系統處理結果的輸出；隱單元是處在輸入和輸出單元之間，不能由系統外部觀察的單元。神經元間的連接權值反映了單元間的連接強度，信息的表示和處理體現在網路處理單元的連接關係中。人工神經網路是一種非程序化、適應性、大腦風格的信息處理，其本質是通過網路的變換和動力學行為得到一種并行分散式的信息處理功能，並在不同程度和層次上模仿人腦神經系統的信息處理功能。它是涉及神經科學、思維科學、人工智慧、計算機科學等多個領域的交叉學科。

人工神經網路是并行分散式系統，採用了與傳統人工智慧和信息處理技術完全不同的機理，克服了傳統的基於邏輯符號的人工智慧在處理直覺、非結構化信息方面的缺陷，具有自適應、自組織和實時學習的特點。

學習是神經網路研究的一個重要內容，它的適應性是通過學習實現的。根據環境的變化，對權值進行調整，改善系統的行為。由Hebb提出的Hebb學習規則為神經網路的學習演演算法奠定了基礎。Hebb規則認為學習過程最終發生在神經元之間的突觸部位，突觸的聯繫強度隨著突觸前後神經元的活動而變化。在此基礎上，人們提出了各種學習規則和演演算法，以適應不同網路模型的需要。有效的學習演演算法，使得神經網路能夠通過連接權值的調整，構造客觀世界的內在表示，形成具有特色的信息處理方法，信息存儲和處理體現在網路的連接中。

分類

根據學習環境不同，神經網路的學習方式可分為監督學習和非監督學習。在監督學習中，將訓練樣本的數據加到網路輸入端，同時將相應的期望輸出與網路輸出相比較，得到誤差信號，以此控制權值連接強度的調整，經多次訓練后收斂到一個確定的權值。當樣本情況發生變化時，經學習可以修改權值以適應新的環境。使用監督學習的神經網路模型有反傳網路、感知器等。非監督學習時，事先不給定標準樣本，直接將網路置於環境之中，學習階段與工作階段成為一體。此時，學習規律的變化服從連接權值的演變方程。非監督學習最簡單的例子是Hebb學習規則。競爭學習規則是一個更複雜的非監督學習的例子，它是根據已建立的聚類進行權值調整。自組織映射、適應諧振理論網路等都是與競爭學習有關的典型模型。

研究神經網路的非線性動力學性質，主要採用動力學系統理論、非線性規劃理論和統計理論，來分析神經網路的演化過程和吸引子的性質，探索神經網路的協同行為和集體計算功能，了解神經信息處理機制。為了探討神經網路在整體性和模糊性方面處理信息的可能，混沌理論的概念和方法將會發揮作用。混沌是一個相當難以精確定義的數學概念。一般而言，“混沌”是指由確定性方程描述的動力學系統中表現出的非確定性行為，或稱之為確定的隨機性。“確定性”是因為它由內在的原因而不是外來的雜訊或干擾所產生，而“隨機性”是指其不規則的、不能預測的行為，只可能用統計的方法描述。混沌動力學系統的主要特徵是其狀態對初始條件的靈敏依賴性，混沌反映其內在的隨機性。混沌理論是指描述具有混沌行為的非線性動力學系統的基本理論、概念、方法，它把動力學系統的複雜行為理解為其自身與其在同外界進行物質、能量和信息交換過程中內在的有結構的行為，而不是外來的和偶然的行為，混沌狀態是一種定態。混沌動力學系統的定態包括：靜止、平穩量、周期性、准同 期性和混沌解。混沌軌線是整體上穩定與局部不穩定相結合的結果，稱之為奇異吸引子。一個奇異吸引子有如下一些特徵：

（1）奇異吸引子是一個吸引子，但它既不是不動點，也不是周期解；

（2）奇異吸引子是不可分割的，即不能分為兩個以及兩個以上的吸引子；

（3）它對初始值十分敏感，不同的初始值會導致極不相同的行為。

1943年，心理學家W.S.McCulloch和數理邏輯學家W.Pitts建立了神經網路和數學模型，稱為MP模型。他們通過MP模型提出了神經元的形式化數學描述和網路結構方法，證明了單個神經元能執行邏輯功能，從而開創了人工神經網路研究的時代。1949年，心理學家提出了突觸聯繫強度可變的設想。60年代，人工神經網路得到了進一步發展，更完善的神經網路模型被提出，其中包括感知器和自適應線性元件等。M.Minsky等仔細分析了以感知器為代表的神經網路系統的功能及局限后，於1969年出版了《Perceptron》一書，指出感知器不能解決高階謂詞問題。他們的論點極大地影響了神經網路的研究，加之當時串列計算機和人工智慧所取得的成就，掩蓋了發展新型計算機和人工智慧新途徑的必要性和迫切性，使人工神經網路的研究處於低潮。在此期間，一些人工神經網路的研究者仍然致力於這一研究，提出了適應諧振理論（ART網）、自組織映射、認知機網路，同時進行了神經網路數學理論的研究。以上研究為神經網路的研究和發展奠定了基礎。1982年，美國加州工學院物理學家J.J.Hopfield提出了Hopfield神經網格模型，引入了“計算能量”概念，給出了網路穩定性判斷。 1984年，他又提出了連續時間Hopfield神經網路模型，為神經計算機的研究做了開拓性的工作，開創了神經網路用於聯想記憶和優化計算的新途徑，有力地推動了神經網路的研究，1985年，又有學者提出了波耳茲曼模型，在學習中採用統計熱力學模擬退火技術，保證整個系統趨於全局穩定點。1986年進行認知微觀結構地研究，提出了并行分佈處理的理論。1986年，Rumelhart, Hinton, Williams發展了BP演演算法。Rumelhart和McClelland出版了《Parallel distribution processing: explorations in the microstructures of cognition》。迄今，BP演演算法已被用於解決大量實際問題。1988年，Linsker對感知機網路提出了新的自組織理論，並在Shanon資訊理論的基礎上形成了最大互信息理論，從而點燃了基於NN的信息應用理論的光芒。1988年，Broomhead和Lowe用徑向基函數(Radial basis function,RBF)提出分層網路的設計方法，從而將NN的設計與數值分析和線性適應濾波相掛鉤。90年代初，Vapnik等提出了支持向量機(Support vector machines, SVM)和VC(Vapnik-Chervonenkis)維數的概念。人工神經網路的研究受到了各個發達國家的重視，美國國會通過決議將1990年1月5日開始的十年定為“腦的十年”，國際研究組織號召它的成員國將“腦的十年”變為全球行為。在日本的“真實世界計算（RWC）”項目中，人工智慧的研究成了一個重要的組成部分。

神經網路的研究可以分為理論研究和應用研究兩大方面。

理論研究可分為以下兩類：

1、利用神經生理與認知科學研究人類思維以及智能機理。

2、利用神經基礎理論的研究成果，用數理方法探索功能更加完善、性能更加優越的神經網路模型，深入研究網路演演算法和性能，如：穩定性、收斂性、容錯性、魯棒性等；開發新的網路數理理論，如：神經網路動力學、非線性神經場等。

應用研究可分為以下兩類：

1、神經網路的軟體模擬和硬體實現的研究。

2、神經網路在各個領域中應用的研究。這些領域主要包括：模式識別、信號處理、知識工程、專家系統、優化組合、機器人控制等。隨著神經網路理論本身以及相關理論、相關技術的不斷發展，神經網路的應用定將更加深入。

人工神經網路的特點和優越性，主要表現在三個方面：

第一，具有自學習功能。例如實現圖像識別時，只在先把許多不同的圖像樣板和對應的應識別的結果輸入人工神經網路，網路就會通過自學習功能，慢慢學會識別類似的圖像。自學習功能對於預測有特別重要的意義。預期未來的人工神經網路計算機將為人類提供經濟預測、市場預測、效益預測，其應用前途是很遠大的。

第二，具有聯想存儲功能。用人工神經網路的反饋網路就可以實現這種聯想。

第三，具有高速尋找優化解的能力。尋找一個複雜問題的優化解，往往需要很大的計算量，利用一個針對某問題而設計的反饋型人工神經網路，發揮計算機的高速運算能力，可能很快找到優化解。

人工神經網路模型主要考慮網路連接的拓撲結構、神經元的特徵、學習規則等。目前，已有近40種神經網路模型，其中有反傳網路、感知器、自組織映射、Hopfield網路、波耳茲曼機、適應諧振理論等。根據連接的拓撲結構，神經網路模型可以分為：

前向網路

網路中各個神經元接受前一級的輸入，並輸出到下一級，網路中沒有反饋，可以用一個有向無環路圖表示。這種網路實現信號從輸入空間到輸出空間的變換，它的信息處理能力來自於簡單非線性函數的多次複合。網路結構簡單，易於實現。反傳網路是一種典型的前向網路。

反饋網路

網路內神經元間有反饋，可以用一個無向的完備圖表示。這種神經網路的信息處理是狀態的變換，可以用動力學系統理論處理。系統的穩定性與聯想記憶功能有密切關係。Hopfield網路、波耳茲曼機均屬於這種類型。

人工神經網路特有的非線性適應性信息處理能力，克服了傳統人工智慧方法對於直覺，如模式、語音識別、非結構化信息處理方面的缺陷，使之在神經專家系統、模式識別、智能控制、組合優化、預測等領域得到成功應用。人工神經網路與其它傳統方法相結合，將推動人工智慧和信息處理技術不斷發展。近年來，人工神經網路正向模擬人類認知的道路上更加深入發展，與模糊系統、遺傳演演算法、進化機制等結合，形成計算智能，成為人工智慧的一個重要方向，將在實際應用中得到發展。將信息幾何應用於人工神經網路的研究，為人工神經網路的理論研究開闢了新的途徑。神經計算機的研究發展很快，已有產品進入市場。光電結合的神經計算機為人工神經網路的發展提供了良好條件。

神經網路在很多領域已得到了很好的應用，但其需要研究的方面還很多。其中，具有分佈存儲、并行處理、自學習、自組織以及非線性映射等優點的神經網路與其他技術的結合以及由此而來的混合方法和混合系統，已經成為一大研究熱點。由於其他方法也有它們各自的優點，所以將神經網路與其他方法相結合，取長補短，繼而可以獲得更好的應用效果。目前這方面工作有神經網路與模糊邏輯、專家系統、遺傳演演算法、小波分析、混沌、粗集理論、分形理論、證據理論和灰色系統等的融合。

下面主要就神經網路與小波分析、混沌、粗集理論、分形理論的融合進行分析。

與小波分析的結合

1981年，法國地質學家Morlet在尋求地質數據時，通過對Fourier變換與加窗Fourier變換的異同、特點及函數構造進行創造性的研究，首次提出了"小波分析"的概念，建立了以他的名字命名的Morlet小波。1986年以來由於YMeyer、S.Mallat及IDaubechies等的奠基工作，小波分析迅速發展成為一門新興學科。Meyer所著的"小波與運算元"，Daubechies所著的"小波十講"是小波研究領域最權威的著作。

小波變換是對Fourier分析方法的突破。它不但在時域和頻域同時具有良好的局部化性質，而且對低頻信號在頻域和對高頻信號在時域里都有很好的解析度，從而可以聚集到對象的任意細節。小波分析相當於一個數學顯微鏡，具有放大、縮小和平移功能，通過檢查不同放大倍數下的變化來研究信號的動態特性。因此，小波分析已成為地球物理、信號處理、圖像處理、理論物理等諸多領域的強有力工具。

小波神經網路將小波變換良好的時頻局域化特性和神經網路的自學習功能相結合，因而具有較強的逼近能力和容錯能力。在結合方法上，可以將小波函數作為基函數構造神經網路形成小波網路，或者小波變換作為前饋神經網路的輸入前置處理工具，即以小波變換的多解析度特性對過程狀態信號進行處理，實現信噪分離，並提取出對加工誤差影響最大的狀態特性，作為神經網路的輸入。

小波神經網路在電機故障診斷、高壓電網故障信號處理與保護研究、軸承等機械故障診斷以及許多方面都有應用，將小波神經網路用於感應伺服電機的智能控制，使該系統具有良好的跟蹤控制性能，以及好的魯棒性，利用小波包神經網路進行心血管疾病的智能診斷，小波層進行時頻域的自適應特徵提取，前向神經網路用來進行分類，正確分類率達到94%。

小波神經網路雖然應用於很多方面，但仍存在一些不足。從提取精度和小波變換實時性的要求出發，有必要根據實際情況構造一些適應應用需求的特殊小波基，以便在應用中取得更好的效果。另外，在應用中的實時性要求，也需要結合DSP的發展，開發專門的處理晶元，從而滿足這方面的要求。

混沌神經網路

混沌第一個定義是上世紀70年代才被Li-Yorke第一次提出的。由於它具有廣泛的應用價值，自它出現以來就受到各方面的普遍關注。混沌是一種確定的系統中出現的無規則的運動，混沌是存在於非線性系統中的一種較為普遍的現象，混沌運動具有遍歷性、隨機性等特點，能在一定的範圍內按其自身規律不重複地遍歷所有狀態。混沌理論所決定的是非線性動力學混沌，目的是揭示貌似隨機的現象背後可能隱藏的簡單規律，以求發現一大類複雜問題普遍遵循的共同規律。

1990年Kaihara、T.Takabe和M.Toyoda等人根據生物神經元的混沌特性首次提出混沌神經網路模型，將混沌學引入神經網路中，使得人工神經網路具有混沌行為，更加接近實際的人腦神經網路，因而混沌神經網路被認為是可實現其真實世界計算的智能信息處理系統之一，成為神經網路的主要研究方向之一。

與常規的離散型Hopfield神經網路相比較，混沌神經網路具有更豐富的非線性動力學特性，主要表現如下：在神經網路中引入混沌動力學行為；混沌神經網路的同步特性；混沌神經網路的吸引子。

當神經網路實際應用中，網路輸入發生較大變異時，應用網路的固有容錯能力往往感到不足，經常會發生失憶現象。混沌神經網路動態記憶屬於確定性動力學運動，記憶發生在混沌吸引子的軌跡上，通過不斷地運動(回憶過程)一一聯想到記憶模式，特別對於那些狀態空間分佈的較接近或者發生部分重疊的記憶模式，混沌神經網路總能通過動態聯想記憶加以重現和辨識，而不發生混淆，這是混沌神經網路所特有的性能，它將大大改善Hopfield神經網路的記憶能力。混沌吸引子的吸引域存在，形成了混沌神經網路固有容錯功能。這將對複雜的模式識別、圖像處理等工程應用發揮重要作用。

混沌神經網路受到關注的另一個原因是混沌存在於生物體真實神經元及神經網路中，並且起到一定的作用，動物學的電生理實驗已證實了這一點。

混沌神經網路由於其複雜的動力學特性，在動態聯想記憶、系統優化、信息處理、人工智慧等領域受到人們極大的關注。針對混沌神經網路具有聯想記憶功能，但其搜索過程不穩定，提出了一種控制方法可以對混沌神經網路中的混沌現象進行控制。研究了混沌神經網路在組合優化問題中的應用。

為了更好的應用混沌神經網路的動力學特性，並對其存在的混沌現象進行有效的控制，仍需要對混沌神經網路的結構進行進一步的改進和調整，以及混沌神經網路演演算法的進一步研究。

基於粗集理論

粗糙集(Rough Sets)理論是1982年由波蘭華沙理工大學教授Z.Pawlak首先提出，它是一個分析數據的數學理論，研究不完整數據、不精確知識的表達、學習、歸納等方法。粗糙集理論是一種新的處理模糊和不確定性知識的數學工具，其主要思想就是在保持分類能力不變的前提下，通過知識約簡，導出問題的決策或分類規則。目前，粗糙集理論已被成功應用於機器學習、決策分析、過程式控制制、模式識別與數據挖掘等領域。

粗集和神經網路的共同點是都能在自然環境下很好的工作，但是，粗集理論方法模擬人類的抽象邏輯思維，而神經網路方法模擬形象直覺思維，因而二者又具有不同特點。粗集理論方法以各種更接近人們對事物的描述方式的定性、定量或者混合性信息為輸入，輸入空間與輸出空間的映射關係是通過簡單的決策表簡化得到的，它考慮知識表達中不同屬性的重要性確定哪些知識是冗餘的，哪些知識是有用的，神經網路則是利用非線性映射的思想和并行處理的方法，用神經網路本身結構表達輸入與輸出關聯知識的隱函數編碼。

在粗集理論方法和神經網路方法處理信息中，兩者存在很大的兩個區別：其一是神經網路處理信息一般不能將輸入信息空間維數簡化，當輸入信息空間維數較大時，網路不僅結構複雜，而且訓練時間也很長；而粗集方法卻能通過發現數據間的關係，不僅可以去掉冗餘輸入信息，而且可以簡化輸入信息的表達空間維數。其二是粗集方法在實際問題的處理中對雜訊較敏感，因而用無雜訊的訓練樣本學習推理的結果在有雜訊的環境中應用效果不佳。而神經網路方法有較好的抑制雜訊干擾的能力。

因此將兩者結合起來，用粗集方法先對信息進行預處理，即把粗集網路作為前置系統，再根據粗集方法預處理后的信息結構，構成神經網路信息處理系統。通過二者的結合，不但可減少信息表達的屬性數量，減小神經網路構成系統的複雜性，而且具有較強的容錯及抗干擾能力，為處理不確定、不完整信息提供了一條強有力的途徑。

目前粗集與神經網路的結合已應用於語音識別、專家系統、數據挖掘、故障診斷等領域，將神經網路和粗集用於聲源位置的自動識別，將神經網路和粗集用於專家系統的知識獲取中，取得比傳統專家系統更好的效果，其中粗集進行不確定和不精確數據的處理，神經網路進行分類工作。

雖然粗集與神經網路的結合已應用於許多領域的研究，為使這一方法發揮更大的作用還需考慮如下問題：模擬人類抽象邏輯思維的粗集理論方法和模擬形象直覺思維的神經網路方法更加有效的結合；二者集成的軟體和硬體平台的開發，提高其實用性。

與分形理論的結合

自從美國哈佛大學數學系教授Benoit B. Mandelbrot於20世紀70年代中期引入分形這一概念，分形幾何學(Fractal geometry)已經發展成為科學的方法論--分形理論，且被譽為開創了20世紀數學重要階段。現已被廣泛應用於自然科學和社會科學的幾乎所有領域，成為現今國際上許多學科的前沿研究課題之一。

由於在許多學科中的迅速發展，分形已成為一門描述自然界中許多不規則事物的規律性的學科。它已被廣泛應用在生物學、地球地理學、天文學、計算機圖形學等各個領域。

用分形理論來解釋自然界中那些不規則、不穩定和具有高度複雜結構的現象，可以收到顯著的效果，而將神經網路與分形理論相結合，充分利用神經網路非線性映射、計算能力、自適應等優點，可以取得更好的效果。

分形神經網路的應用領域有圖像識別、圖像編碼、圖像壓縮，以及機械設備系統的故障診斷等。分形圖像壓縮/解壓縮方法有著高壓縮率和低遺失率的優點，但運算能力不強，由於神經網路具有并行運算的特點，將神經網路用於分形圖像壓縮/解壓縮中，提高了原有方法的運算能力。將神經網路與分形相結合用於果實形狀的識別，首先利用分形得到幾種水果輪廓數據的不規則性，然後利用3層神經網路對這些數據進行辨識，繼而對其不規則性進行評價。

分形神經網路已取得了許多應用，但仍有些問題值得進一步研究：分形維數的物理意義；分形的計算機模擬和實際應用研究。隨著研究的不斷深入，分形神經網路必將得到不斷的完善，並取得更好的應用效果。

人工神經網路的構築理念是受到生物（人或其他動物）神經網路功能的運作啟發而產生的。人工神經網路通常是通過一個基於數學統計學類型的學習方法（Learning Method）得以優化，所以人工神經網路也是數學統計學方法的一種實際應用，通過統計學的標準數學方法我們能夠得到大量的可以用函數來表達的局部結構空間，另一方面在人工智慧學的人工感知領域，我們通過數學統計學的應用可以來做人工感知方面的決定問題(也就是說通過統計學的方法，人工神經網路能夠類似人一樣具有簡單的決定能力和簡單的判斷能力)，這種方法比起正式的邏輯學推理演算更具有優勢。

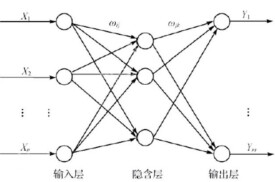
神經網路近來越來越受到人們的關注，因為它為解決大複雜度問題提供了一種相對來說比較有效的簡單方法。神經網路可以很容易的解決具有上百個參數的問題（當然實際生物體中存在的神經網路要比我們這裡所說的程序模擬的神經網路要複雜的多）。神經網路常用於兩類問題：分類和回歸。在結構上，可以把一個神經網路劃分為輸入層、輸出層和隱含層（見圖1）。輸入層的每個節點對應一個個的預測變數。輸出層的節點對應目標變數，可有多個。在輸入層和輸出層之間是隱含層（對神經網路使用者來說不可見），隱含層的層數和每層節點的個數決定了神經網路的複雜度。

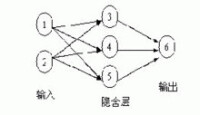
除了輸入層的節點，神經網路的每個節點都與很多它前面的節點（稱為此節點的輸入節點）連接在一起，每個連接對應一個權重Wxy，此節點的值就是通過它所有輸入節點的值與對應連接權重乘積的和作為一個函數的輸入而得到，我們把這個函數稱為活動函數或擠壓函數。如圖2中節點4輸出到節點6的值可通過如下計算得到：

W14*節點1的值+W24*節點2的值

神經網路的每個節點都可表示成預測變數（節點1，2）的值或值的組合（節點3-6）。注意節點6的值已經不再是節點1、2的線性組合，因為數據在隱含層中傳遞時使用了活動函數。實際上如果沒有活動函數的話，神經元網路就等價於一個線性回歸函數，如果此活動函數是某種特定的非線性函數，那神經網路又等價於邏輯回歸。

調整節點間連接的權重就是在建立（也稱訓練）神經網路時要做的工作。最早的也是最基本的權重調整方法是錯誤回饋法，現在較新的有變化坡度法、類牛頓法、Levenberg-Marquardt法、和遺傳演演算法等。無論採用那種訓練方法，都需要有一些參數來控制訓練的過程，如防止訓練過度和控制訓練的速度。

決定神經網路拓撲結構（或體系結構）的是隱含層及其所含節點的個數，以及節點之間的連接方式。要從頭開始設計一個神經網路，必須要決定隱含層和節點的數目，活動函數的形式，以及對權重做那些限制等，當然如果採用成熟軟體工具的話，他會幫你決定這些事情。在諸多類型的神經網路中，最常用的是前向傳播式神經網路，也就是我們前面圖示中所描繪的那種。人們下面詳細討論一下，為討論方便假定只含有一層隱含節點。可以認為錯誤回饋式訓練法是變化坡度法的簡化，其過程如下：前向傳播：數據從輸入到輸出的過程是一個從前向後的傳播過程，后一節點的值通過它前面相連的節點傳過來，然後把值按照各個連接權重的大小加權輸入活動函數再得到新的值，進一步傳播到下一個節點。

回饋：當節點的輸出值與我們預期的值不同，也就是發生錯誤時，神經網路就要“學習”（從錯誤中學習）。我們可以把節點間連接的權重看成后一節點對前一節點的“信任”程度（他自己向下一節點的輸出更容易受他前面哪個節點輸入的影響）。學習的方法是採用懲罰的方法，過程如下：如果一節點輸出發生錯誤，那麼他看他的錯誤是受哪個（些）輸入節點的影響而造成的，是不是他最信任的節點（權重最高的節點）陷害了他（使他出錯），如果是則要降低對他的信任值（降低權重），懲罰他們，同時升高那些做出正確建議節點的信任值。對那些收到懲罰的節點來說，他也需要用同樣的方法來進一步懲罰它前面的節點。就這樣把懲罰一步步向前傳播直到輸入節點為止。

對訓練集中的每一條記錄都要重複這個步驟，用前向傳播得到輸出值，如果發生錯誤，則用回饋法進行學習。當把訓練集中的每一條記錄都運行過一遍之後，人們稱完成一個訓練周期。要完成神經網路的訓練可能需要很多個訓練周期，經常是幾百個。訓練完成之後得到的神經網路就是在通過訓練集發現的模型，描述了訓練集中響應變數受預測變數影響的變化規律。

由於神經網路隱含層中的可變參數太多，如果訓練時間足夠長的話，神經網路很可能把訓練集的所有細節信息都“記”下來，而不是建立一個忽略細節只具有規律性的模型，我們稱這種情況為訓練過度。顯然這種“模型”對訓練集會有很高的準確率，而一旦離開訓練集應用到其他數據，很可能準確度急劇下降。為了防止這種訓練過度的情況，人們必須知道在什麼時候要停止訓練。在有些軟體實現中會在訓練的同時用一個測試集來計算神經網路在此測試集上的正確率，一旦這個正確率不再升高甚至開始下降時，那麼就認為現在神經網路已經達到做好的狀態了可以停止訓練。

神經網路在訓練周期增加時準確度的變化情況

神經元網路和統計方法在本質上有很多差別。神經網路的參數可以比統計方法多很多。如圖4中就有13個參數（9個權重和4個限制條件）。由於參數如此之多，參數通過各種各樣的組合方式來影響輸出結果，以至於很難對一個神經網路表示的模型做出直觀的解釋。實際上神經網路也正是當作“黑盒”來用的，不用去管“盒子”裡面是什麼，只管用就行了。在大部分情況下，這種限制條件是可以接受的。比如銀行可能需要一個筆跡識別軟體，但他沒必要知道為什麼這些線條組合在一起就是一個人的簽名，而另外一個相似的則不是。在很多複雜度很高的問題如化學試驗、機器人、金融市場的模擬、和語言圖像的識別，等領域神經網路都取得了很好的效果。

神經網路的另一個優點是很容易在并行計算機上實現，可以把他的節點分配到不同的CPU上并行計算。

在使用神經網路時有幾點需要注意：第一，神經網路很難解釋，目前還沒有能對神經網路做出顯而易見解釋的方法學。

第二，神經網路會學習過度，在訓練神經網路時一定要恰當的使用一些能嚴格衡量神經網路的方法，如前面提到的測試集方法和交叉驗證法等。這主要是由於神經網路太靈活、可變參數太多，如果給足夠的時間，他幾乎可以“記住”任何事情。

第三，除非問題非常簡單，訓練一個神經網路可能需要相當可觀的時間才能完成。當然，一旦神經網路建立好了，在用它做預測時運行時還是很快得。

第四，建立神經網路需要做的數據準備工作量很大。一個很有誤導性的神話就是不管用什麼數據神經網路都能很好的工作並做出準確的預測。這是不確切的，要想得到準確度高的模型必須認真的進行數據清洗、整理、轉換、選擇等工作，對任何數據挖掘技術都是這樣，神經網路尤其注重這一點。比如神經網路要求所有的輸入變數都必須是0-1（或-1--+1）之間的實數，因此像“地區”之類文本數據必須先做必要的處理之後才能用作神經網路的輸入。

人工神經網路在信息領域中的應用

在處理許多問題中，信息來源既不完整，又包含假象，決策規則有時相互矛盾，有時無章可循，這給傳統的信息處理方式帶來了很大的困難，而神經網路卻能很好的處理這些問題，並給出合理的識別與判斷。

1.信息處理

現代信息處理要解決的問題是很複雜的，人工神經網路具有模仿或代替與人的思維有關的功能，可以實現自動診斷、問題求解，解決傳統方法所不能或難以解決的問題。人工神經網路系統具有很高的容錯性、魯棒性及自組織性，即使連接線遭到很高程度的破壞，它仍能處在優化工作狀態，這點在軍事系統電子設備中得到廣泛的應用。現有的智能信息系統有智能儀器、自動跟蹤監測儀器系統、自動控制制導系統、自動故障診斷和報警系統等。

2. 模式識別

模式識別是對錶征事物或現象的各種形式的信息進行處理和分析，來對事物或現象進行描述、辨認、分類和解釋的過程。該技術以貝葉斯概率論和申農的資訊理論為理論基礎，對信息的處理過程更接近人類大腦的邏輯思維過程。現在有兩種基本的模式識別方法，即統計模式識別方法和結構模式識別方法。人工神經網路是模式識別中的常用方法，近年來發展起來的人工神經網路模式的識別方法逐漸取代傳統的模式識別方法。經過多年的研究和發展，模式識別已成為當前比較先進的技術，被廣泛應用到文字識別、語音識別、指紋識別、遙感圖像識別、人臉識別、手寫體字元的識別、工業故障檢測、精確制導等方面。

人工神經網路在醫學中的應用

由於人體和疾病的複雜性、不可預測性，在生物信號與信息的表現形式上、變化規律（自身變化與醫學干預后變化）上，對其進行檢測與信號表達，獲取的數據及信息的分析、決策等諸多方面都存在非常複雜的非線性聯繫，適合人工神經網路的應用。目前的研究幾乎涉及從基礎醫學到臨床醫學的各個方面，主要應用在生物信號的檢測與自動分析，醫學專家系統等。

1. 生物信號的檢測與分析

大部分醫學檢測設備都是以連續波形的方式輸出數據的，這些波形是診斷的依據。人工神經網路是由大量的簡單處理單元連接而成的自適應動力學系統，具有巨量并行性，分散式存貯，自適應學習的自組織等功能，可以用它來解決生物醫學信號分析處理中常規法難以解決或無法解決的問題。神經網路在生物醫學信號檢測與處理中的應用主要集中在對腦電信號的分析，聽覺誘發電位信號的提取、肌電和胃腸電等信號的識別，心電信號的壓縮，醫學圖像的識別和處理等。

2. 醫學專家系統

傳統的專家系統，是把專家的經驗和知識以規則的形式存儲在計算機中，建立知識庫，用邏輯推理的方式進行醫療診斷。但是在實際應用中，隨著資料庫規模的增大，將導致知識“爆炸”，在知識獲取途徑中也存在“瓶頸”問題，致使工作效率很低。以非線性并行處理為基礎的神經網路為專家系統的研究指明了新的發展方向，解決了專家系統的以上問題，並提高了知識的推理、自組織、自學習能力，從而神經網路在醫學專家系統中得到廣泛的應用和發展。在麻醉與危重醫學等相關領域的研究中，涉及到多生理變數的分析與預測，在臨床數據中存在著一些尚未發現或無確切證據的關係與現象，信號的處理，干擾信號的自動區分檢測，各種臨床狀況的預測等，都可以應用到人工神經網路技術。

人工神經網路在經濟領域的應用

1. 市場價格預測

對商品價格變動的分析，可歸結為對影響市場供求關係的諸多因素的綜合分析。傳統的統計經濟學方法因其固有的局限性，難以對價格變動做出科學的預測，而人工神經網路容易處理不完整的、模糊不確定或規律性不明顯的數據，所以用人工神經網路進行價格預測是有著傳統方法無法相比的優勢。從市場價格的確定機制出發，依據影響商品價格的家庭戶數、人均可支配收入、貸款利率、城市化水平等複雜、多變的因素，建立較為準確可靠的模型。該模型可以對商品價格的變動趨勢進行科學預測，並得到準確客觀的評價結果。

2. 風險評估

風險是指在從事某項特定活動的過程中，因其存在的不確定性而產生的經濟或財務的損失、自然破壞或損傷的可能性。防範風險的最佳辦法就是事先對風險做出科學的預測和評估。應用人工神經網路的預測思想是根據具體現實的風險來源，構造出適合實際情況的信用風險模型的結構和演演算法，得到風險評價係數，然後確定實際問題的解決方案。利用該模型進行實證分析能夠彌補主觀評估的不足，可以取得滿意效果。

人工神經網路在控制領域中的應用

人工神經網路由於其獨特的模型結構和固有的非線性模擬能力，以及高度的自適應和容錯特性等突出特徵，在控制系統中獲得了廣泛的應用。其在各類控制器框架結構的基礎上，加入了非線性自適應學習機制，從而使控制器具有更好的性能。基本的控制結構有監督控制、直接逆模控制、模型參考控制、內模控制、預測控制、最優決策控制等。

人工神經網路在交通領域的應用

今年來人們對神經網路在交通運輸系統中的應用開始了深入的研究。交通運輸問題是高度非線性的，可獲得的數據通常是大量的、複雜的，用神經網路處理相關問題有它巨大的優越性。應用範圍涉及到汽車駕駛員行為的模擬、參數估計、路面維護、車輛檢測與分類、交通模式分析、貨物運營管理、交通流量預測、運輸策略與經濟、交通環保、空中運輸、船舶的自動導航及船隻的辨認、地鐵運營及交通控制等領域並已經取得了很好的效果。

人工神經網路在心理學領域的應用

從神經網路模型的形成開始，它就與心理學就有著密不可分的聯繫。神經網路抽象於神經元的信息處理功能，神經網路的訓練則反映了感覺、記憶、學習等認知過程。人們通過不斷地研究，變化著人工神經網路的結構模型和學習規則，從不同角度探討著神經網路的認知功能，為其在心理學的研究中奠定了堅實的基礎。近年來，人工神經網路模型已經成為探討社會認知、記憶、學習等高級心理過程機制的不可或缺的工具。人工神經網路模型還可以對腦損傷病人的認知缺陷進行研究，對傳統的認知定位機制提出了挑戰。

雖然人工神經網路已經取得了一定的進步，但是還存在許多缺陷，例如：應用的面不夠寬闊、結果不夠精確；現有模型演演算法的訓練速度不夠高；演演算法的集成度不夠高；同時我們希望在理論上尋找新的突破點，建立新的通用模型和演演算法。需進一步對生物神經元系統進行研究，不斷豐富人們對人腦神經的認識。