z檢驗
用於推斷差異發生概率的方法
Z檢驗(Z Test)是一般用於大樣本(即樣本容量大於30)平均值差異性檢驗的方法。它是用標準正態分佈的理論來推斷差異發生的概率,從而比較兩個平均數的差異是否顯著。在國內也被稱作u檢驗。
當已知標準差時,驗證一組數的均值是否與某一期望值相等時,用Z檢驗。
z檢驗又叫u檢驗
第一步:建立虛無假設,即先假定兩個平均數之間沒有顯著差異。
第二步:計算統計量Z值,對於不同類型的問題選用不同的統計量計算方法。
1、如果檢驗一個樣本平均數x與一個已知的總體平均數μ的差異是否顯著。其Z值計算公式為:
其中:
x是檢驗樣本的平均數;
μ是已知總體的平均數;
S是總體的標準差;
n是樣本容量。
2、如果檢驗來自兩個的兩組樣本平均數的差異性,從而判斷它們各自代表的總體的差異是否顯著。其Z值計算公式為:
其中:
,是樣本1,樣本2的平均數;
是樣本1,樣本2的標準差;
是樣本1,樣本2的容量。
第三步:比較計算所得Z值與理論Z值,推斷髮生的概率,依據Z值與差異顯著性關係表作出判斷。如下表所示:
| Z | P值 | 差異程度 |
| 非常顯著 | ||
| 顯著 | ||
| 不顯著 |
第四步:根據是以上分析,結合具體情況,作出結論。
Z檢驗舉例
某項教育技術實驗,對實驗組和控制組的前測和后測的數據分別如下表所示,比較兩組前測和后測是否存在差異。
實驗組和控制組的前測和后測數據表
前測 實驗組
控制組
后測 實驗組
控制組
由於,屬於大樣本,所以採用Z檢驗。由於這是檢驗來自兩個不同總體的兩個樣本平均數,看它們各自代表的總體的差異是否顯著,所以採用雙總體的Z檢驗方法。
計算前要測Z的值:
∴ 前測兩組差異不顯著。
再計算后測Z的值:
∴ 后測兩組差異顯著。
語法
描述
X為樣本值,M為,sigma為標準差,ALPHA為顯著性水平。時,表示備擇假設為“期望值不等M”(雙邊檢驗);時,表示備擇假設為“期望值大於M”(單邊檢驗);時,表示備擇假設為“期望值小於M”(單邊檢驗)。
SIG為當原假設為真時得到的觀察值的概率,當SIG為小概率的時候則對原假設提出置疑。表示在顯著水平為ALPHA的情況下,不能拒絕原假設;表示在顯著性水平為ALPHA的情況下,拒絕原假設。
舉例
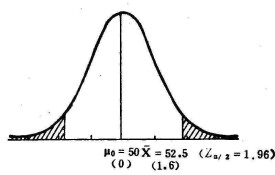
例題:給定一組某廠生產的紐扣直徑的數據,假設其直徑,已知,並且在標準情況下,紐扣的平均直徑應該是,問:是否可以認為這批紐扣的直徑符合標準?()
解:總體均值和已知,則,問題就化為根據樣本值來判斷還是,為此提出假設:
原假設:
備擇假設:
Matlab實現過程如下:
程序運行結果如下:
x=
Columns 1 through 6
26.0100 26.0000 25.9800 25.8600 26.3200 25.5800
Columns 7 through 10
25.3200 25.8900 26.3200 26.1800
程序運行結果如下:
H=
SIG=
0.9622
結果,說明在0.05的水平下,不能拒絕原假設,即認為這批紐扣的直徑符合標準。
(1)已知,檢驗
選擇統計量
在 成立的假定下,服從 分佈,對給定的顯著性水平,查標準正態分佈表可得臨界值,使得
這說明
為小概率事件。將樣本值代入算出統計量的值。如果,則表明在一次試驗中小概率事件 出現了,因而拒絕,接受。在以上的假設檢驗問題中,當構造小概率事件時,利用了統計量 的概率密度曲線兩側尾部的面積,這樣的檢驗稱為雙側檢驗。這裡採用雙側檢驗有直觀的解釋:因為任何情況下,都是未知參數 的無偏估計,所以當 成立時,即 時,與 不應相差太大。因此,對於固定的樣本容量,如果 太大,則有理由懷疑 的正確性,從而認為 與 有顯著差別。大到什麼程度才有足夠的理由拒絕 呢?這需要由給定的顯著性水平 查得的臨界值 來決定。
(2)已知,檢驗
選擇統計量
並令
則. 若 成立,還有
對給定的,由標準正態分佈表可得臨界值,使得
即
這說明事件“”為小概率事件。因此的拒絕域為. 將樣本值代入算出統計量的值,若,則拒絕,接受;否則可接受。
在以上的假設檢驗問題中,當構造小概率事件時,利用了的分佈概率密度曲線的單側尾部的面積,這樣的檢驗稱為單邊檢驗。直觀解釋是:如果 成立,即 比 的值就不能大得太多。因此,對於固定的樣本容量,如果太大,則有理由懷疑 的正確性。至於大到什麼程度才有足夠的理由拒絕 呢?這需要由給定的顯著性水平 查得的臨界值來決定。