無約束優化方法
無約束優化方法
無約束優化方法是研究尋求多元函數ƒ(尣)=ƒ(x1,x2,…,xn)在整個實n維空間Rn中局部極小值點的數值方法。它在非線性規劃的研究中佔有很重要的位置,除了本身的意義與應用外,它也是許多帶約束優化方法的基礎。
目錄
大多數無約束優化方法都是迭代法,每一次迭代都從某一點尣 移到另一個適合條件
移到另一個適合條件
無約束優化方法
ƒ(尣)<ƒ(尣 ) (1)
) (1)
無約束優化方法
的點尣。為了得到尣,首先要確定移動的方向 s ,其次要確定沿方向 s
,其次要確定沿方向 s 移動的步長λk,於是尣=尣
移動的步長λk,於是尣=尣 +λks
+λks 。對應於s
。對應於s 與λk的不同選取,就得到不同的演演算法。
與λk的不同選取,就得到不同的演演算法。
無約束優化方法
無約束優化方法
無約束優化方法
無約束優化方法
無約束優化方法
直接法 往往以直觀或以計算實踐為基礎而產生,這類演演算法的特點是只要求計算函數值本身,因而易於使用,但是與另一些要求計算偏導數值的方法相比,又收斂得慢。所以直接法常常用於變數極少而函數比較複雜且不易計算偏導數的情形。較為常用的直接法有鮑威爾法、單純形調優法和模式搜索法。
最陡下降法和牛頓-拉弗森方法 在要求計算偏導函數值的演演算法類中,一般取移動方向s 滿足
滿足
無約束優化方法
無約束優化方法
這裡的T表示矩陣(或向量)的轉置運算,墷ƒ(尣)表示ƒ(尣)在點尣上的梯度,即
。
式(2)保證了在以尣 為始點,s
為始點,s 為方向的半直線
為方向的半直線
無約束優化方法
無約束優化方法
(3)
上一定有點尣適合ƒ(尣)<ƒ(尣 )。為了使式(2)成立,往往取
)。為了使式(2)成立,往往取
無約束優化方法
, (4)
式中Hk是一n階的對稱正定矩陣。
通常,步長λk的選取原則是取λk使尣為ƒ(x)在半直線(3)上的最小值點。這樣選取步長 λk的過程稱為精確線性搜索或簡稱線性搜索。這時有
, (5)
亦即點尣上的梯度方向與移動方向成正交。
只要墷ƒ(尣 )≠0,總可以按上述方法進行迭代。在一定的假設下,能夠證明墷ƒ(尣
)≠0,總可以按上述方法進行迭代。在一定的假設下,能夠證明墷ƒ(尣 )→0,於是對於凸函數ƒ(尣),點列{尣
)→0,於是對於凸函數ƒ(尣),點列{尣 }的任何極限點都是ƒ(尣)的最小值點;而對於一般的非凸函數,即使不能保證{尣
}的任何極限點都是ƒ(尣)的最小值點;而對於一般的非凸函數,即使不能保證{尣 }的極限點是局部最小值點,但因目標函數值逐次減少,往往也能得到滿意的結果。
}的極限點是局部最小值點,但因目標函數值逐次減少,往往也能得到滿意的結果。
無約束優化方法
無約束優化方法
無約束優化方法
無約束優化方法
可以證明,在由尣 出發的所有同樣長度的方向中,負梯度方向是使函數值下降最快的方向。於是取移動方向s
出發的所有同樣長度的方向中,負梯度方向是使函數值下降最快的方向。於是取移動方向s 為負梯度方向-墷ƒ(尣
為負梯度方向-墷ƒ(尣 ),或者等價地取(4)中的Hk為單位矩陣I,並由線性搜索確定步長λk與下一點尣。這就是通常所謂的最陡下降法。
),或者等價地取(4)中的Hk為單位矩陣I,並由線性搜索確定步長λk與下一點尣。這就是通常所謂的最陡下降法。
無約束優化方法
無約束優化方法
無約束優化方法
牛頓-拉弗森法則以 ƒ(尣)的二次近似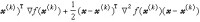 為基礎,在二階偏導數矩陣墷2ƒ(x
為基礎,在二階偏導數矩陣墷2ƒ(x )為正定時,以此二次近似的最小值點為下一點,即取
)為正定時,以此二次近似的最小值點為下一點,即取
無約束優化方法
無約束優化方法
,
但這樣得到的 尣 未必適合式(1),因此又改成以為移動方向,或者等價地在(4)中取Hk為(墷2ƒ(尣 ))-1,再通過線性搜索來確定 λk與尣。
))-1,再通過線性搜索來確定 λk與尣。
無約束優化方法
在一些有關ƒ(尣)的假設下,對於這兩個古老的方法,都可證明墷ƒ(尣 )→0。這兩個方法各有其優缺點。最陡下降法比較簡單,並且除了函數值本身外,只需要計算一階偏導數的值;但是理論分析和計算實踐都表明這個方法的收斂速度很慢。事實上,由 及式(5)可知,{尣
)→0。這兩個方法各有其優缺點。最陡下降法比較簡單,並且除了函數值本身外,只需要計算一階偏導數的值;但是理論分析和計算實踐都表明這個方法的收斂速度很慢。事實上,由 及式(5)可知,{尣 }中的點沿著相互正交的方向交替前進,因此,即使對於二次嚴格凸函數
}中的點沿著相互正交的方向交替前進,因此,即使對於二次嚴格凸函數
無約束優化方法
無約束優化方法
, (6)
式中A對稱正定,只要A不是數量矩陣αI,那麼尣 就曲折前進,且進展很慢。當n=2時如圖
就曲折前進,且進展很慢。當n=2時如圖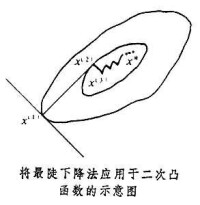 所示。
所示。
無約束優化方法

無約束優化方法
與此相反,牛頓-拉弗森方法收斂得快。特別對於形如(6)的二次嚴格凸函數,只要一次迭代,就能達到最優解尣*,即使對於一般的函數ƒ(尣),在某些假設下,也可證明{尣 }為二階收斂。這個方法不僅要計算 n個一階偏導數,而且還要計算個二階偏導數,因此只在n比較小或函數比較簡單的情形才使用。
}為二階收斂。這個方法不僅要計算 n個一階偏導數,而且還要計算個二階偏導數,因此只在n比較小或函數比較簡單的情形才使用。
無約束優化方法
共軛梯度法與變尺度法是既有較快的收斂速度又無需計算二階偏導函數的演演算法。
共軛梯度法 由於在局部最小值點的鄰近,函數的性狀與二次凸函數 (6)十分相似,所以對於一個好的尋優方法,人們要求它在應用於二次凸函數時有較快的收斂速度,即使最小值點不能象牛頓-拉弗森方法那樣一步達到,也應在有限步內達到。事實上,沿著y空間中n個兩兩正交的方向依次作線性搜索,一定可以達到函數1/2 (y-y*)T(y-y*) 的最小值點y*。於是通過變換y=A1/2尣,沿著尣空間中n個滿足
(7)
的方向s(1),s(2),…,s(n)依次作線性搜索,就一定能達到函數(6)的最小值點尣*。滿足式(7)的n個非零方向 s(1),s(2),…,s(n)稱為關於矩陣A的共軛方向系。20世紀60年代R.弗萊徹和C.M.里夫斯用梯度向量構造出共軛方向系,提出了共軛梯度法。它從任意的初始點尣(1)開始,在第k次迭代時取移動方向
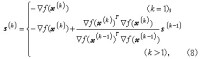
無約束優化方法
無約束優化方法
無約束優化方法
無約束優化方法
而若不採取周期性重開始的策略,其收斂階僅為線性。共軛梯度法由於只需要存貯幾個向量,特別適宜於解大型問題。當然,還需要採用條件予優的方法以加速收斂。
變尺度方法 也有人稱為擬牛頓方法。這是近二十多年來發展起來的一類很有成效的尋優方法。理論分析和計算實踐都表明這類方法的收斂速度較快,同時又無需計算二階偏導數矩陣。這類方法的共同特點是:移動方向s 由(4)定義,其中Hk為n階對稱正定方陣;H1可以任意選取,但通常取H1=I;當k>1時,Hk由Hk-1和
由(4)定義,其中Hk為n階對稱正定方陣;H1可以任意選取,但通常取H1=I;當k>1時,Hk由Hk-1和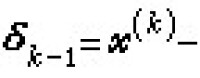 以及確定,並滿足如下的擬牛頓方程
以及確定,並滿足如下的擬牛頓方程
無約束優化方法
無約束優化方法
(9)
步長λk和下一點尣由線性搜索確定。
第一個變尺度法是W.D.戴維登於1959年首先提出的,而由 R.弗萊徹和 M.J.D.鮑威爾在理論上作了研究並於1963年公開發表,所以通常稱為dfp方法,在這個方法中,Hk(k>1)的定義如下:
。
由於DFP方法的成功,在其後十多年間,又提出了許多變尺度方法,這些方法只在Hk(k>1)的定義方法上有所不同。在理論上,只要尣 、H1取得相同,那麼在一定條件下,由不同的變尺度方法產生的點列{尣
、H1取得相同,那麼在一定條件下,由不同的變尺度方法產生的點列{尣 }都只依賴於某一參數;但在實際計算中,由於舍入誤差的關係,由不同的變尺度方法產生的點列未盡相同。最成功的變尺度法是BFGS法,它的Hk(k>1)定義為 與DFP方法相比,BFGS方法具有較好的數值穩定性。
}都只依賴於某一參數;但在實際計算中,由於舍入誤差的關係,由不同的變尺度方法產生的點列未盡相同。最成功的變尺度法是BFGS法,它的Hk(k>1)定義為 與DFP方法相比,BFGS方法具有較好的數值穩定性。
無約束優化方法
無約束優化方法
無論是DFP方法或者 BFGS方法,都有以下一些性質:①只要初始的矩陣H1正定,那麼以後的各個矩陣Hk(k≥1)也都正定;②將它們應用於二次嚴格凸函數(6)時,由演演算法所確定的移動方向序列s(1),s(2),…,s(n)是一組關於矩陣A的共軛方向系,所以最多經過n次迭代,一定能夠達到二次嚴格凸目標函數的最小點尣*;③理論上可以證明這兩個演演算法在一定的條件下都是超線性收斂並且都是n步二階收斂的。
不精確線性搜索或可接受點準則 前述各法都是建立在線性搜索的基礎之上的,即取尣恰為ƒ(尣)在半直線(3)上的最小值點,但在實際計算中,無法做到;雖然可以用黃金分割、二次插值等方法做到充分的近似,卻極為費時。近年來,人們注意建立在不精確線性搜索的基礎之上的方法。鮑威爾於1976年證明了:用適當的不精確線性搜索代替線性搜索后,BFGS演演算法仍是超線性收斂的。80年代,又出現了信賴域方法和基於錐模型的優化演演算法,已取得了良好的效果,受到了廣泛的重視。
最小平方和問題 一類具有特殊形式的無約束優化問題。在這類問題中,目標函數ƒ(尣)是一些函數的平方和,即。這類問題在數據擬合中經常出現,方程組的求解也可轉化為最小平方和的問題。由於目標函數具有特殊的形式,所以人們設計了專門的方法,如高斯-牛頓方法、萊文貝格-馬夸特方法等。
參考書目
R.Fletcher,Prαcticαl Methods of Optimizαtion,Unconstrαined Optimizαtion, Vol.1, John Wiley &Sons, New York, 1979.
