均勻形核
均勻形核
對液體的一種簡單而實用的看法是將其想像為隨機分佈的硬球構成。液體中原子間的距離與晶態相相近,但在液相中每個原子的平均最相鄰原子數比晶體的少。因而結構較為開放,並且其原子比固態有較大的活動性。整個液體內布滿著細小的、緊密堆垛的、堆垛排列與固態相似的原子團。由於結構的開放性,這些原子團可快速地形成與消散。原子團尺寸與穩定性之間的關係取決於溫度。
為導出一種簡單的有關尺寸與穩定性之間關係的計演演算法,我們作兩個假設。第一,原子團與液體間界面的能量為各向同性的,即與形成此界面的特定晶面無關。這樣的限制暗示形成的相是球形的。第二,單位表面的界面能與固相尺寸無關。雖然大多數情況下轉變產物的顯微結構並不是球狀的,但採用簡單的幾何形狀的模型,經過不大的修改就可應用於實際系統。
與液-固轉變相關的自由能變化包含著兩個特定的部分:第一部分是與形成液-固界面相關的能量變化,第二部分是液、固相體積自由能的差別。球形顆粒的總界面能是界面積()與單位面積界面能(γ)之積。下圖(a)顯示因存在內界面使系統的自由能隨生長相半徑的變化關係。
第二項能量項是體積自由能。它是固相和液相的自由能差乘以顆粒的體積。對於,固相的體積自由能比液相低,的自由能變化是負值。如下圖(b)所示,單位體積自由能與體積之積隨著半徑增大而越來越低。
總的自由能變化為表面能項與體積自由能項之和。加和的結果如下圖(c)所示。要注意這兩個能量項朝著相反的方向變化。開始時r面積項起支配作用,當顆粒變得比較大時總自由能量增加。然而,一旦達到臨界半徑后,r體積項就開始起支配作用,顆粒半徑進一步增加導致系統自由能下降。這樣,就存在一個穩定核的臨界半徑,即較小的將溶入液相而較大的顆粒將繼續長大。
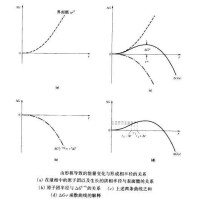
均勻形核
前面指出,在過冷的液體中並不是所有的晶胚都可以轉變成為晶核,只有那些尺寸等於或大於某一臨界尺寸的晶胚才能穩定的存在,並能自發地長大。這種等於或大於臨界尺寸的晶胚即為晶核。為什麼過冷液體形核要求晶核具有一定的臨界尺寸,這需要從形核時的能量變化進行分析。
在一定的過冷度條件下,固相的自由能低於液相的自由能,當在此過冷液體中出現晶胚時,一方面原子從液態轉變為固態將使系統的自由能降低,它是結晶的驅動力;另一方面,由於晶胚構成新的表面,形成表面能,從而使系統的自由能升高,它是結晶的阻力。若晶胚的體積為V,表面積為S,固、液兩相單位體積自由能差為,單位面積表面能為σ,則系統自由能的總變化為:
上式右端的第一項是液體中出現晶胚時所引起的體積自由能的變化,如果是過冷液體,則為負值,否則為正值。第二項是液體中出現晶胚時所引起的表面能變化,這一項總是正值。顯然,第一項的絕對值越大,越有利於結晶;第二項的絕對值越小,也越有利於結晶。為了計算上的方便,假設過冷液體中出現一個半徑為r的球狀晶胚,它所引起的自由能變化為:
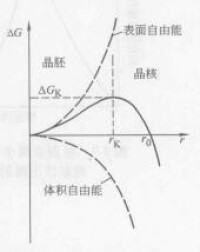
晶粒半徑與△G的關係
由能的減小將佔優勢。於是在與r的關係曲線上出現了一個極大值,與之相對應的r值為r。由圖可知,當時,隨著晶胚尺寸r的增大,則系統的自由能增加,顯然這個過程不能自動進行,這種晶胚不能成為穩定的晶核,而是瞬時形成,又瞬時消失。但當時,則隨著晶胚尺寸的增大,伴隨著系統自由能的降低,這一過程可以自動進行,晶胚可以自發地長大成穩定的晶核,因此它將不再消失。當時,這種晶胚既可能消失,也可能長大成為穩定的晶核,因此把半徑為的晶胚稱為臨界晶核,稱為臨界晶核半徑。
晶胚尺寸達到臨界尺寸時,體系總的自由能仍然大於零,而的晶胚已能穩定存在並開始長大。原因是系統內部能提供一部分額外能量以克服形核能壘,這部分額外能量來自母相中的能量起伏、結構起伏和成分起伏。因此,時相變不一定能進行;時相變不一定不能進行。
綜上所述,是形核的必要條件,母相中存在的能量起伏、結構起伏和成分起伏是形核的充分條件。
只要增強體與析出相之間沒有化學交互作用,均勻形核的析出相不會受增強體的影響。在Al—Li合金中,獨立地在結構缺陷處形核的共格相就是一個很好的例子。但是有點奇怪的是,掃描差熱分析的試驗數據說明在SiC增強體的作用下,δ相析出的放熱只有少量的偏移。而實際上SiC顆粒促進了合金中的時效硬化(就像在未經增強的合金中塑性變形促進時效硬化一樣)。另外,透射電鏡的證據說明,在這兩種情況下,析出相尺寸及其在空間的密度變化並沒有受到影響。在未經增強的合金中,與硬化峰對應的δ相尺寸約為30μm,從能量上看,這一尺寸大於對Orowan硬化是比切割顆粒更有利的尺寸,而在複合材料中,硬度的峰值則在更小的析出相尺寸處出現(約20nm),這一事實說明,時效硬化的加速可能與δ相無關,而與別的因素有關。在顆粒/基體界面處的析出相貧化區可能與此有關。
均勻形核理論可以用一系列公式及圖形表示,利用這些公式進行定量計算與實際情況會有較大的差別,但是可利用均勻形核理論對一些相變問題進行定性解釋。根據簡單的模型,得到下面關於固態相變形核的一些基本規律:
①只有的降低,形核過程才能進行。由於多出一項應變能,所以固態相變比液態結晶的阻力大。
②在形核過程中存在一個極值尺寸的晶核,當晶核的尺寸為時,晶核尺寸減少或者增加,都導致下降。
③如果形成晶核尺寸小於,當有原子附加到該晶核上將引起自由焓增加,所以不可能進行,意味著這種“小尺寸”的晶核不能夠長大。從這個意義上說,即使母相中存在這種“小尺寸”的晶核,也不能說已經開始形核。
④如果形成晶核尺寸等於,當有原子附加上這樣的晶核后使,導致下降,意味著長大可以降低自由焓,所以它就成為一個實際存在的晶核。這種尺寸的晶核就被稱為臨界尺寸晶核。形成臨界尺寸晶核所增加的自由焓稱為臨界晶核形成功。
⑤減少界面能及應變能,均可使臨界形核功變小,易於形核。
⑥當形核尺寸大於,如果有原子附加到這樣的晶核上,也會使減少,也可使晶核持續長大。但是新相與母相一般在結構或成分有所不同。尺寸越大,要求在母相中出現與新相相同結構或成分的區域就越困難。從這個角度分析,r*是最容易形成晶核的尺寸。
⑦因為形核率,與溫度呈指數變化關係,當變化不大時,會引起形核率急劇變化。而的大小依賴於驅動力,驅動力又是隨溫度變化的,這導致形核率,隨過冷度激烈變化。雖然形核率在開始時隨過冷度加大迅速增加,但由於Q幾乎與溫度無關,所以,在很大過冷時,形核率又重新降低,出現極值現象。