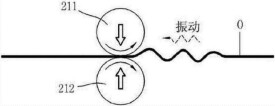
物體的振動

物體圍繞一平衡位置的往返重複運動。物體的一部分或整體受力的作用產生形變，形變部分具有恢復其原來狀態的力(恢復力，或稱具有形變勢能)。例如固體的彈性力和液體的表面張力等都可成為恢復力，此外還可以有外加的恢復力，例如把弦或膜拉緊的張力等。在外加作用力消失后，恢復力使變形的物體向平衡位置運動，形變勢能逐漸轉化為動能，在物體達到平衡位置時，形變勢能為零而動能最大；由於慣性作用，物體繼續沿與原形變方向相反的方向偏離平衡位置，產生新的形變，動能逐漸轉化為形變勢能，在動能為零時形變勢能最大，偏離平衡位置的距離也最大。如此重複，形成物體的振動。

實際常見的物體振動 可以理想化地分為弦、棒、膜、板和殼的振動。

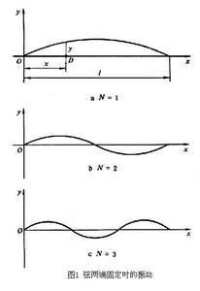
把一根長度為 Л的柔軟（無剛性）且尺度和質量完全均勻的弦拉緊並兩端固定（圖1a），用手指輕彈弦即可激起弦的橫振動。它的振動方程為， (1)

式中y為弦上坐標x為的一點D在橫方向的位移，單位為米(m)，t是時間，單位為秒(s)，с是波動在弦上傳播的速度，單位為米每秒(m/s)， (2)

F是弦上的張力，單位為牛【頓】(N)，d是弦的線密度，單位為千克每米()。弦自由振動時的頻率為， (3)

式中。時頻率最低，稱為基頻，對應的振動方式稱為一次諧波；時稱為二次諧波（圖1b），依次類推。可見二次以上的高次諧波的頻率是基頻的整數倍。在穩定振動的情況下，弦中的波是駐波（見波），因此次諧波除兩端固定無位移外，弦上還有個無位移的點（圖1b、圖1c），稱之為節點。而位移最大的部分稱為波腹。根據式(3)可知，改變弦的長度Л或張力或線密度，都可以改變弦振動的頻率。弦樂器如胡琴、琵琶和提琴等，都是根據弦的這個振動原理製成的。

物體的振動

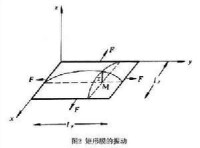
一個柔軟無剛性的薄膜，厚度及質量完全均勻，如果它周邊用力向外拉緊並固定，即形成一個可以振動的膜。常見的膜周邊的形狀是矩形和圓形。考慮如圖2中所示的矩形膜。若膜平面為平面，是膜上坐標為(,)的一個點，膜振動時點離開它靜止時位置的位移為，於是可得膜的振動方程為， (4)

式中(5)是波動在膜中傳播的速度，F是膜邊緣上每單位長度上的張力，單位為牛頓每米(N/m)，δ是膜的面密度，單位為千克每平方米()，t是時間。式(4)表明膜是二維的“弦”。膜的振動頻率為， (6)

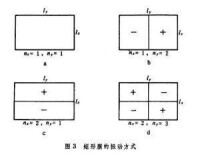
式中、和是矩形膜的邊長。當時，膜的振動頻率最低，是基頻(圖3a)。當，時，膜的振動方式如圖3b所示，除周邊外還有一個縱向的節線(其上諸點的位移為零)，節線把膜分成左右兩部分，在振動時兩部分的相位相反，即在一邊向上運動時另一邊向下運動。當，時，膜被一橫節線分成相位相反的兩部分(圖3c)。只有當 時，膜的振動頻率是基頻的整數倍，即高次諧波。而時，振動頻率是基頻的泛音。

物體的振動

物體的振動

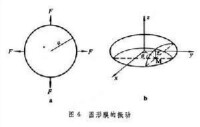
圖4所示是半徑為的圓形膜，用柱坐標表示它的振動方程為。 (7)

為膜上點M的極坐標，z為M點的位移。圓形膜自由振動時的頻率為， (8)

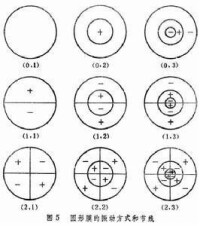
其中，是無量綱的常數，隨不同的m、m而異。表中給出幾種振動方式的頻率，而,是圓膜振動時的基頻。其他頻率都不是基頻的整數倍，是它的泛音。圓膜振動時的振動方式及節線如圖5所示。

物體的振動

物體的振動

物體的振動

橫截面尺度小於長度的固體稱為棒或梁。棒受作用力的擾動后可以產生振動，稱為棒的振動。其形式因受力方式而異，一般有縱振動、彎曲振動和扭轉振動三種。棒或梁的剛性可以支撐它本身的重量，故不像弦那樣必須在兩端固定拉緊才能振動，只需把棒架起即可使棒產生振動。

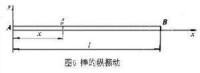
棒的縱振動　對各向同性密度均勻的材料製成的細棒，用錘沿棒軸方向輕擊一端表面的中心，如圖6所示，即可激起棒的縱振動，振動時棒中質點的運動方向與棒軸平行。棒的振動方程是， (9)

式中ξ 是距端處棒截面的位移。根據棒兩端的情況，棒可以有不同的振動形式。一般有三種，即棒兩端全是自由的、兩端全是固定的和一端自由一端固定三種情況。兩端都是自由的棒振動頻率為， (10)

式中l是棒長， ，是細棒中縱波傳播速度，。其振動方式如圖7b所示，縱坐標表示振動時棒各部分的位移。圖中也給出節點的位置。圖7a是兩端固定的棒的振動方式，從圖可看出其振動頻率與兩端自由的棒振動頻率相同，只是節點的位置不同。一端固定一端自由的棒縱振動時的頻率為。

(11)

與式(10)相比，可知一端固定另一端自由的棒，作縱振動時的基頻只為兩端自由或兩端固定時的頻率的一半，而且只有奇次諧波。

物體的振動

物體的振動棒的彎曲振動　沿與棒垂直的方向擊棒，可激起棒的彎曲振動，振動時的形狀如圖8所示。棒做彎曲振動時的振動方程是， (12)

式中 k是棒橫截面的迴轉半徑。與棒縱振動的情形類似，其振動頻率也與棒兩端的邊界條件有關。一般端點條件有兩種情況：即棒的一端自由，另一端固定；棒兩端都是自由的。根據兩端的條件解式(12)，可得一端自由一端固定的棒做彎曲振動時的頻率為，

，

，

……。

兩端自由的棒彎曲振動時的頻率為，

，

，

……。

物體的振動

在樂器中有些是利用棒的振動原理製成的，例如木琴、風琴的簧片、調音用的音叉等。

從以上所列頻率看，棒做彎曲振動時，它的泛音都不是基頻的整數倍。

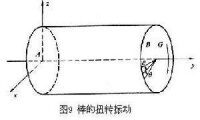
棒的扭轉振動 棒除了能作縱振動和彎曲振動外，還可以作扭轉振動，如圖9所示。若截面為圓形的棒端的面與平面吻合併固定，棒軸與軸吻合，在端加一扭矩，使面上的半徑轉過一個角，然後撤去扭矩, 則棒即可做扭轉振動。棒的每個截面都以軸為圓心往返轉動。扭轉振動的方程為， (13)

式中с是無限固體中橫波傳播速度，是角位移。因面固定，故無角位移，即節點。這與一端固定另一端自由的棒做縱振動時的頻率相似，於是有，

物體的振動

適當增加膜的厚度可以形成薄板，薄板振動時的恢復力主要來自板的剛性，而不像膜是來自外加的張力。生活中常見的振動薄板多為圓形，如傳聲器或電話耳機中的薄金屬片，樂器中的鑼、鈸、鐃等。

均勻薄板對稱振動時的振動方程是， (15)

式中,z是薄板與xy平面吻合時在z方向的位移，k是面迴轉半徑，對於厚度為的均勻薄板， ，E是板材的彈性模量，是體密度，是泊松比(物體受力拉長時，橫向單位長度收縮值與縱向單位長度拉長值之比)，是用極坐標時拉普拉斯算符。圓形薄板振動時的頻率與周邊支撐情況有關，假設板做簡諧振動，圓板周邊在處固定，形成節線，則頻率的表達式是。 (16)

用上式求得的基頻及泛音頻率為，

，

，

……。

將板彎曲成殼體，可以製成鍾、磬、鈴等發聲的樂器。發聲的殼多用金屬製成，其振動頻率與殼體的形狀、尺寸、彈性和密度有關，除少數形狀十分簡單的殼體比較容易求出其振動頻率外，對形狀複雜的殼體，計算它的振動頻率是比較繁難的。瑞利曾對長度大於直徑並均勻的圓柱形殼體振動時的頻率進行計算，算得的振動頻率為， (17)

式中,為殼體的厚度，K為體積模量，a為殼體的半徑，s為殼體圓周對波長的倍數，即殼體圓周上的波節數為2s。

一般殼體樂器如鐘磬等的橫剖面均為圓形，但在中國出土文物中的古代編鐘的橫剖面卻為橢圓形，而且表面上還有古書中稱為“枚”的圓柱形乳突，用現代科學技術分析中國古代編鐘的聲學特性，結果表明橢圓形狀及表面上的“枚”對鐘的音質都有一定的作用。節線的位置及分佈也符合科學原理。出土的編鐘均完好無損，這一切都說明早在西周時代（公元前1066～前771）,中國人已在樂器製造和合金冶鍊方面有了相當高的工藝和技術水平。