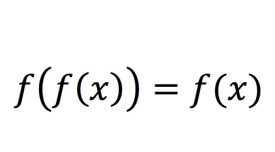冪等

在數學里，冪等有兩種主要的定義。

在某二元運算下，冪等元素是指被自己重複運算(或對於函數是為複合)的結果等於它自己的元素。例如，乘法下僅有兩個冪等實數，為0和1。

某一元運算為 冪等的時，其作用在任一元素兩次後會和其作用一次的結果相同。例如，高斯符號便是冪等的。

一元運算的定義是二元運算定義的特例

設 S為一具有作用於其自身的二元運算的集合，則 S的元素 s稱為冪等的(相對於*)當

s * s = s.

特別的是，任一單位元都是冪等的。若 S的所有元素都是冪等的話，則其二元運算*被稱做是冪等的。例如，聯集和交集的運算便都是冪等的。

設 f為一由 X映射至 X的一元運算，則 f為冪等的，當對於所有在 X內的 x，

f( f( x)) = f( x).

特別的是，恆等函數一定是冪等的，且任一常數函數也都是冪等的。

注意當考慮一由 X至 X的所有函數所組成的集合 S時。在 f在一元運算下為冪等的若且唯若在二元運算下， f相對於其複合運算(標記為 o)會是冪等的。這可以寫成 f o f = f。

如上述所說，恆等函數和常數函數總會是冪等的。較不當然的例子有實數或複數引數的絕對值函數，以及實數引數的高斯符號。

將一拓撲空間 X內各子集 U映射至 U閉包的函數在 X的冪集上是冪等的。這是閉包運算元的一個例子；所有個閉包運算元都會是冪等函數。

定義上，環的冪等元素為一相對於環乘法為冪等的元素。可以定義一於環冪等上的偏序：若e和f為冪等的，當ef= fe= e時，標記為e≤ f。依其順序，0會是最小冪等元素，而1為最大冪等元素。

若 e在環 R內為冪等的，則 eRe一樣會是個乘法單位元為 e的環。

兩個冪等元素 e和 f被稱為 正交的當 ef= fe=0。在此一情形下， e+ f也是冪等的，且有 e ≤ e + f和 f ≤ e + f。

若 e在環 R內為冪等的，則 f = 1 − e也會是冪等的，且 e和 f正交。

一在 R內的冪等元素 e稱為 核心的，若對所有在 R內的 x， ex= xe。在此情形之下， Re會是個乘法單位元為 e的環。 R的核心冪等元素和 R的分解為環的直和有很直接的關接。若 R為環 R、...、 R的直和，則環 R的單位元在 R內為核心冪等的，相互正交，且其總和為1。相反地，給出 R內給相互正交且總和為1的核心冪等元素 e、...、 e，則 R會是環 Re、...、 Re的直和。所有較有趣的是，每一於 R內的核心冪等 e都會給出一 R的分解－ Re和 R(1 − e)的直和。

任一不等於0和1的冪等元素都是零因子(因為 e(1 − e) = 0)。這表示了整環及除環都不會存在此種冪等元素。局部環也沒有此種冪等元素，但理由有點不同。唯一包含於一環的雅各布森根內的冪等元素只有0。共四元數環內會有一冪等元素組成的懸鏈曲面。

所有元素都冪等的環稱做布爾環。可證明在每一此類環內，乘法都是可交換的，且每一元素都有其各自的加法逆元。

冪等運算也可以在布林代數內找到。邏輯和與邏輯或便都是冪等運算。

在線性代數里，投射是冪等的。亦即，每一將向量投射至一子空間V(不需正交)上的線性運算元，都是冪等的。

一冪等半環為其 加法(非乘法)為冪等的半環。