輻角主值
輻角主值
複數的模與輻角是複數三角形式表示的兩個基本元素,複數所對應的向量長度稱為複數的幅值,該向量與實軸正方向的夾角為複數的輻角。輻角的大小有無窮多,但是輻角主值唯一確定。
由於一個複數可以由有序實數對 唯一確定,而有序實數對與平面直角坐標系中的點一一對應,因此可以用坐標為的點P 來表示該複數,此時x 軸上的點與實數對應,稱x 軸為實軸,y 軸上的點(除原點外)與純虛數對應,稱 y軸為虛軸,像這樣表示複數的平面稱為複平面。
複數還可以用向量 來表示, x與 y分別是向量在 x軸與y 軸上的投影。這樣,複數z 就與平面上的向量 建立了一一對應的關係。
向量的長度稱為複數 的模或絕對值,記作,於是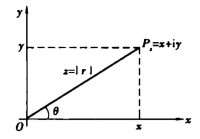

輻角主值
當點 P 不是原點,即複數 時,向量 與 x軸正向的夾角稱為複數 的輻角,記作Argz 。輻角的符號規定為:由正實軸依反時針方向轉到 為正,依順時針方向轉到 為負。
顯然一個非零複數 z的輻角有無窮多個值,它們相差2Π 的整數倍,但 Argz中只有一個值v0 滿足條件,稱 為複數 z的主輻角,記為argz ,於是
當 時,z 的輻角沒有意義。
複數的 輻角是以x軸的正半軸為始邊,向量OZ所在的 射線(起點是O)為終邊的角θ。任意一個不為零的複數的輻角有無限多個值,且這些值相差2π的整數倍。把適合於的輻角θ的值,叫做輻角的主值,記作argz。輻角的主值是唯一的。且有。
複數的主輔角argz與反正切的主值有以下關係
