漸伸線
漸伸線
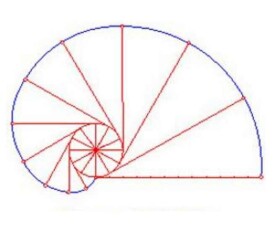
漸伸線(evolvent),也稱漸近線。與一條曲線C的所有切線相交成直角的曲線Γ,稱為曲線C的漸伸線。當一根繩正沿著另一曲線繞上或脫下時,它描出一條漸伸線。漸伸線的形狀見於鷹嘴、鯊魚背鰭和棕櫚樹懸葉尖端。機器齒輪,齒兩側曲線(齒郭曲線)大多採用漸伸線。
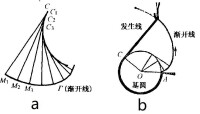
圖1
一條直線在一個圓上作無滑動的滾動時,直線上一定點運動的軌跡稱為“圓的漸伸線”,而稱該圓為漸伸線的“基圓”,直線為漸伸線的“發生線”,如圖1(b)所示。即若在圓周繞有無彈性的細繩,且保持這個圓固定不動,而將細繩拉緊並逐漸展開,,讓該線繞圓軸運動且始終與圓軸相切,那麼線上一個定點在該平面上的軌跡就是漸伸線。
漸伸線的形狀僅取決於基圓的大小,基圓越小,漸伸線越彎曲;基圓越大,漸伸線越平直;基圓為無窮大時,漸伸線為斜直線。
若基圓的半徑為r,以基圓圓心為原點建立坐 標系,則可得漸開線的參數方程:
式中,為定點與圓心連線和X軸間的夾角。
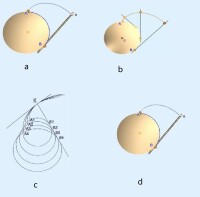
圖2
(1)漸開線的發生線展直前後長度不變,即發生線沿 基圓滾過的長度等於基圓上被滾過的弧長,如圖2(a)中,弧。
(2)漸開線上任一點的法線必與基圓相切。KB為漸開線在K點的法線,發生線沿基圓作純滾動,所以線段為漸開線上點的法線,且必與基圓相切。B是漸開線K點處的曲率中心,BK是曲率半徑;A處的曲率半徑為0。漸開線各點的曲率半徑是變化的,K點離基圓越遠,曲率半徑越大,漸開線形狀越平緩。如圖2(b).
(3)漸開線的形狀取決於基圓的大小,同一基圓上的漸開線形狀完全相同。基圓越大漸開線越平直,基圓半徑為無窮大時,漸開線就成為直線,如圖2(c)。
(4)因漸開線是從基圓開始向外展開的,故基圓以內無漸開線;漸開線上各點壓力角不相等。離基圓越遠,壓力角越大。如圖2(d)。
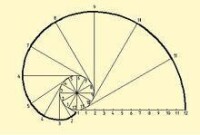
圖3
(2)畫法2:已知圓的直徑D,如圖3所示,畫漸伸線的方法為:
1)將圓周分成若干等分(圖中為12等分),將周長作相同等分;
2)過周長上各等分點作圓的切線;
3)在第一條切線上,自切點起量取周長的一個等分()得點1;在第二條切線上,自切點起量取周長的兩個等分()得點2;依此類推得點3、4、……、12;
4)用曲線板光滑連接點1、2、3、……、12。即得圓的漸伸線。
5)以此類推,可以畫出圓第二圈、第三圈、...的漸伸線。
機器齒輪齒兩側曲線(齒郭曲線)大多採用漸伸線,以獲得穩定轉動比,保證運轉平穩,減小震動,稱為漸開線齒輪。