HMMs
HMMs
HMMs是指隱馬爾科夫模型,是一種演演算法模型,用於語言信號處理,是對語音信號的時間序列結構建立統計模型。
為了分析語音信號而提出的一個演演算法模型。在語音信號處理上用的比較多
隱馬爾可夫模型(HMMs)是對語音信號的時間序列結構建立統計模型,可將之看作一個數學上的雙重隨機過程:一個是用具有有限狀態數的Markov鏈來模擬語音信號統計特性變化的隱含的隨機過程,另一個是與Markov鏈的每一個狀態相關聯的觀測序列的隨機過程。前者通過後者表現出來,但前者的具體參數是不可測的。人的言語過程實際上就是一個雙重隨機過程,語音信號本身是一個可觀測的時變序列,是由大腦根據語法知識和言語需要(不可觀測的狀態) 發出的音素的參數流。可見HMM合理地模仿了這一過程,很好地描述了語音信號的整體非平穩性和局部平穩性,是較為理想的一種語音模型。從整段語音來看,人類語音是一個非平穩的隨機過程,但是若把整段語音分割成若干短時語音信號,則可認為這些短時語音信號是平穩過程,我們就可以用線性手段對這些短時語音信號進行分析。若對這些語音信號建立隱馬爾可夫模型,則可以辯識具有不同參數的短時平穩的信號段,並可以跟蹤它們之間的轉化,從而解決了對語音的發音速率及聲學變化建立模型的問題。
HMMS(HyperMedia Management Schema) WBEM的一部分
是一種可擴展的,獨立於實現的公共數據描述模式。它能夠描述,實例化和訪問各種數據,是對各種被管對象的高層抽象。它由核心模式和特定域模式兩層構成,核心模式由高層的類以及屬性 關聯組成、將被管理環境分成被管系統元素、應用部件和網路部件。特定域模式繼承了核心模式,採用其基本的語義定義某一特定環境的對象。
1.1 離散馬爾可夫過程
在一個環環相扣的隨機變數的序列中,每個隨機變數以多大的概率取什麼值,僅僅與它前面一個變數有關,而與它更前面的變數無關。
在已知“現在”的的條件下,“未來”與“過去”彼此獨立的特性就被稱為馬爾科夫性,具有這種性質的隨機過程就叫做馬爾科夫過程,其最原始的模型就是馬爾科夫鏈。
用一個通俗的比喻來形容,一隻被切除了大腦的白鼠在若干個洞穴間的躥動就構成一個馬爾科夫鏈。因為這隻白鼠已沒有了記憶,瞬間而生的念頭決定了它從一個洞穴躥到另一個洞穴;當其所在位置確定時,它下一步躥往何處與它以往經過的路徑無關。這一模型的哲學意義是十分明顯的,用前蘇聯數學家辛欽(1894-1959〕的話來說,就是承認客觀世界中有這樣一種現象,其未來由現在決定的程度,使得我們關於過去的知識絲毫不影響這種決定性。
1.2 隱馬爾可夫模型的要素
隱馬爾可夫模型由五個要素組成,其中兩個狀態集合(N、M),三個概率矩陣(A、B、π):
1)N,表示模型中的狀態數,狀態之間可以相互轉移。
2)M,表示每個狀態不同的觀察符號,即輸出字元的個數。
3)A,狀態轉移概率分佈。
4)B,觀察符號在各個狀態下的概率分佈。
5)π,表示初始狀態分佈。
給定N,M,A,B, π,HMMs能夠輸出一個觀察符號序列,這個序列的元素屬於M。
因為隱馬爾可夫模型由兩個狀態集合和三個概率矩陣構成,所以HMMs可以形式化定義為一個五元組(N,M,A,B,π)。
1.3 隱馬爾可夫模型的IPO模型
輸入:HMMs的五元組(N,M,A,B,π)。
輸出:一個觀察符號的序列,這個序列的每個元素都是M中的元素。
1.4 實例一
一個隱士也許不能夠直接獲取到天氣的觀察情況,但是他有一些水藻。民間傳說告訴我們水藻的狀態與天氣狀態有一定的概率關係——天氣和水藻的狀態是緊密相關的。在這個例子中我們有兩組狀態,觀察的狀態(水藻的狀態)和隱藏的狀態(天氣的狀態)。我們希望為隱士設計一種演演算法,在不能夠直接觀察天氣的情況下,通過水藻和馬爾科夫假設來預測天氣。
例子中,需要著重指出的是,隱藏狀態的數目與觀察狀態的數目可以是不同的。一個包含三個狀態的天氣系統(晴天、多雲、雨天)中,可以觀察到4個等級的海藻濕潤情況(干、稍干、潮濕、濕潤)。
在這種情況下,觀察到的狀態序列與隱藏過程有一定的概率關係。我們使用隱馬爾科夫模型對這樣的過程建模,這個模型包含了一個底層隱藏的隨時間改變的馬爾科夫過程,以及一個與隱藏狀態某種程度相關的可觀察到的狀態集合。
下圖顯示的是天氣例子中的隱藏狀態和觀察狀態。假設隱藏狀態(實際的天氣)由一個簡單的一階(即只與前一個變數有關)馬爾科夫過程描述,那麼它們之間都相互連接。隱藏狀態和觀察狀態之間的連接表示:在給定的馬爾科夫過程中,一個特定的隱藏狀態生成特定的觀察狀態的概率。這很清晰的表示了‘進入’一個觀察狀態的所有概率之和為1,在上面這個例子中就是Pr(Obs|Sun), Pr(Obs|Cloud) 及 Pr(Obs|Rain)之和。
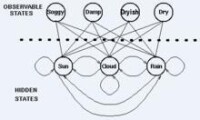
HMMs
注意矩陣的每一行之和是1。
我們已經看到在一些過程中一個觀察序列與一個底層馬爾科夫過程是概率相關的。在這些例子中,觀察狀態的數目可以和隱藏狀態的數碼不同。
我們使用一個隱馬爾科夫模型(HMM)對這些例子建模。這個模型包含兩組狀態集合和三組概率集合:
* 隱藏狀態:一個系統的(真實)狀態,可以由一個馬爾科夫過程進行描述(例如,天氣)。
* 觀察狀態:在這個過程中‘可視’的狀態(例如,海藻的濕度)。
*狀態轉移矩陣:包含了一個隱藏狀態到另一個隱藏狀態的概率
*混淆矩陣:包含了給定隱馬爾科夫模型的某一個特殊的隱藏狀態,觀察到的某個觀察狀態的概率。
因此一個隱馬爾科夫模型是在一個標準的馬爾科夫過程中引入一組觀察狀態,以及其與隱藏狀態間的一些概率關係。
1.5 實例二
假設你有一個住得很遠的朋友,他每天跟你打電話告訴你他那天做了什麼。你的朋友僅僅對三種活動感興趣:公園散步,購物以及清理房間。他選擇做什麼事情只憑天氣。你對於他所住的地方的天氣情況並不了解,但是你知道總的趨勢。在他告訴你每天所做的事情基礎上,你想要猜測他所在地的天氣情況.
你認為天氣的運行就像一個馬爾可夫鏈.其有兩個狀態 "雨"和"晴",但是你無法直接觀察它們,也就是說,它們對於你是隱藏的。每天,你的朋友有一定的概率進行下列活動:"散步", "購物", 或 "清理". 因為你朋友告訴你他的活動,所以這些活動就是你的觀察數據。這整個系統就是一個隱馬爾可夫模型HMM.
你知道這個地區的總的天氣趨勢,並且平時知道你朋友會做的事情。也就是說這個隱馬爾可夫模型的參數是已知的。你可以用程序語言(Python)寫下來:
states = ('Rainy', 'Sunny') #模型中的狀態集合N observations = ('walk', 'shop', 'clean') #每個狀態不同的觀察符號Mstart_probability = {'Rainy': 0.6, 'Sunny': 0.4} #初始狀態分佈π#狀態轉移概率分佈Atransition_probability = { 'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3}, 'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6}, } #觀察符號在各個狀態下的概率分佈Bemission_probability = { 'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5}, 'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1}, }
在這些代碼中,start_probability代表了你對於你朋友第一次給你打電話時的天氣情況的不確定性(你知道的只是那個地方平均起來下雨多些).在這裡,這個特定的概率分佈並非平衡的,平衡概率應該接近(在給定變遷概率的情況下){'Rainy': 0.571, 'Sunny': 0.429}
1.6 HMMs的應用
一旦一個系統可以作為HMM被描述,就可以用來解決三個基本問題。其中前兩個是模式識別的問題:給定HMM求一個觀察序列的概率(評估);搜索最有可能生成一個觀察序列的隱藏狀態序列(解碼)。第三個問題是給定觀察序列生成一個HMM(學習)。
1)評估,考慮這樣的問題,我們有一些描述不同系統的HMMs及一個觀察序列。我們想知道哪一個HMMs模型最有可能產生這個給定的觀察序列。也就是通過HMMs來求給定序列的概率,哪個概率大,我們就認為是哪個HMMs。
2)解碼,這個問題是我們最感興趣的,因為,我們對隱藏狀態序列更加感興趣,所以,我們想通過給定的HMMs模型及觀察序列來確定隱藏狀態序列。
3)學習,這個問題是最難的,根據觀察序列以及一個隱藏狀態集合,來估計一個最合適的HMMs模型,當狀態轉移矩陣和混淆矩陣不能被直接測量時,我們可以用向前向後演演算法來估計參數。
1.7 HMMs總結
由一個向量和兩個矩陣(pi,A,B)描述的隱馬爾可夫模型對於實際系統有著巨大的價值,雖然經常只是一種近似,但他們是經得起分析的,HMMs通常解決的問題有:
1)對於一個觀察序列匹配一個最可能的系統----評估,使用向前演演算法(forward algorithm)解決。
2)對於已生成的觀察序列,確定最可能的隱藏狀態序列----解碼,使用維特比演演算法(Viterbi algorithm)解決。
3)對於已有的觀察序列,決定最有可能的模型參數----學習,使用向前向後演演算法(forward backward algorithm)解決。
HMMs的缺點:HMMs的一些假設過於簡單。
目錄