極坐標法
解決幾何中曲線方程的方法
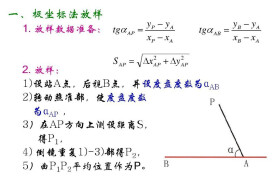
極坐標法是在控制點上測設一個角度和一段距離來確定點的平面位置。
極坐標法
用極坐標解決幾何問題的方法。在直角坐標系中(),x被代替,y被代替,,從而得到新的方程。這樣的方程常常用來解決曲線問題,如橢圓曲線、紐線、螺線等等,可以使解題更加清晰簡便。
設曲線C的極坐標方程為。
則C的參數方程為
其中θ為極角。
極坐標法
設曲線C在點處的極半徑OM與切線MT間的夾角為Ψ,則(如圖)
故有
將yˊ代入,化簡得
這一重要公式表明:在極坐標系下,曲線的極半徑r(θ)與其導數rˊ(θ)之比等於極半徑與曲線切線之夾角的正切。
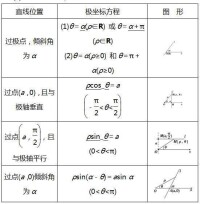
極坐標方程經常會表現出不同的對稱形式,如果,則曲線關於極點()對稱,如果,則曲線關於極點()對稱,如果,則曲線相當於從極點逆時針方向旋轉。
在
極坐標系中,圓心在()半徑為R的圓的方程為:
該方程可簡化為不同的方法,以符合不同的特定情況,比如方程r=a表示一個以極點為中心半徑為a的圓。
經過極點的射線由如下方程表示:
,
其中φ為射線的傾斜角度,若m為直角坐標系的射線的斜率,則有。任何不經過極點的直線都會與某條射線垂直。這些在點()處的直線與射線垂直,其方程為。

方程為 r
坐標的玫瑰線(polarrose)是數學曲線中非常著名的曲線,看上去像花瓣,它只能用極坐標方程來描述,方程如下:
或
,
如果k是整數,當k是奇數時那麼曲線將會是k個花瓣,當k是偶數時曲線將是2k個花瓣。如果k為非整數,將產生圓盤(disc)狀圖形,且花瓣數也為非整數。注意:該方程不可能產生4的倍數加2(如2,6,10……)個花瓣。變數a代表玫瑰線花瓣的長度。
右圖為方程r(θ)
的一條阿基米德螺線。
阿基米德螺線在極坐標里使用以下方程表示:,
改變參數a將改變螺線形狀,b控制螺線間距離,通常其為常量。阿基米德螺線有兩條螺線,一條,另一條。兩條螺線在極點處平滑地連接。把其中一條翻轉°得到其鏡像,就是另一條螺線。
圓錐曲線方程如下:
其中l表示半徑,e表示離心率。如果,曲線為橢圓,如果,曲線為拋物線,如果,則表示雙曲線。
或者
其中e表示離心率,p表示焦點到準線的距離。
極坐標提供了一個表達開普勒行星運行定律的自然數的方法。

極坐標法
圖2極坐標法測定界址點
採用極坐標法測量時,界址點坐標可按下式計算:
其中:——待測界址點坐標
——測站點已知坐標
——測站點至待測界址點距離
——已知方位角
——觀測角
直角坐標
互相垂直,並且有公共原點的數軸。其中橫軸為X軸,縱軸為Y軸。這樣我們就說在平面上建立了平面直角坐標系,簡稱直角坐標系
球坐標是三維坐標系的一種,用以確定三維空間中點、線、面以及體的位置,它以坐標原點為參考點,由方位角、仰角和距離構成。
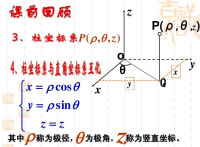
柱坐標系
柱坐標系中的三個坐標變數是r、φ、z。與直角坐標系相同,柱坐標系中也有一個z變數。各變數的變化範圍是:
其中