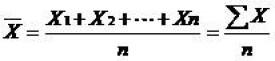算術均數

算術均數（簡稱算數均數）是描述一組同質觀察值的集中趨勢，反映一組觀察值平均水平的三種常用指標之一（其餘為幾何均數和中位數），適用於服從對稱分佈變數的平均水平描述。

將所有的觀察值直接相加，再除以總例數，其計算公式為：其中，n為樣本均數，為觀察值。式中的在不引起混淆的前提下，可簡化為或者。

加權法（頻率表法）

加權法是根據頻數表計算均數的一種方法。當觀察例數較多時，資料通常要分組編成頻數表，對已經編成頻數表的資料不能再用直接法計算，這種情況我們可以把各組的組中值視為各組觀察值的代表值，分別乘以各組的頻數得到各組觀察值之和，然後將它們相加得到觀察值的總和再除以總例數。其計算公式如下：

式中k表示頻數表的組段數，為第k組段的頻數，為第k組段的組中值，，分別為第k組段的上限值與下限值。

1、算術平均數是一個良好的描述集中趨勢的指標，具有反應靈敏、確定嚴密、簡明易解、計算簡單、適合進一步演算和較小受抽樣變化的影響等優點。

2、算術平均數易受極端數據的影響，這是因為平均數反應靈敏，每個數據的或大或小的變化都會影響到最終結果。

3、算術均數與方差有著密不可分的關係。

實例：

某年某醫院8名女性晚期癌症患者紅細胞計數（）為。是求其算術均數。