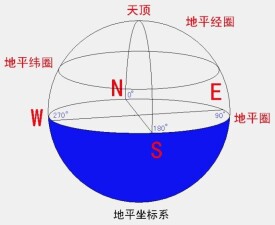
地平坐標系
直觀的天球坐標系
地平坐標系是一種最直觀的天球坐標系,和我們日常的天文觀測關係最為密切。
例如,在晴朗的傍晚,觀測者經常可以看到人造衛星在群星間的運行,和大量的流星現象,它們的運行速度都很快,記錄衛星或流星的位置最簡便的方法就是記下某瞬間該衛星或流星的地平方位角和地平高度角,這就是我們所要討論的地平坐標系。
地平坐標系
地平圈就是觀測者所在的地平面無限擴展與天球相交的大圓。從觀測者所在的地點,作垂直於地平面的直線並無限延長,在地平面以上與天球相交的點,稱為天頂;在地平面以下與天球相交的點,稱為天底。在天球上,天頂和天底與地平圈的角距離均為90°,只不過一個在地平圈以上,另一個在地平圈以下。地平圈把天球分為可見半球和不可見半球兩部分。
由於天球的半徑是任意長的,而地球的半徑則相對很小,因此,觀測者所在的點可以認為是與地心重合的,地平圈也可以看成是以地心為圓心的,這與觀測者所在點的地平面在天球上是完全一致的。
地軸的無限延長即為天軸,天軸與天球有兩個交點,與地球北極相對應的那個點叫做北天極,與地球南極相對應的那個點叫做南天極。通過天頂和北天極的地平經圈(當然也通過天底和南天極),與地平圈有兩個交點;靠近天北極的地個點為北點,靠近天南極的那個點為南點。北點和南點分別把地平圈和地平經圈等分。根據面北背南、左西右東的原則,可以確定當地的東點和西點,即面向北點左90°為西點,右90°為東點。這樣,就確定了地平圈上的東、西、南、北四方點。
在地平坐標系中,通過南點、北點的地平經圈稱子午圈。子午圈被天頂、天底等分為兩個180°的半圓。以北點為中點的半個圓弧,稱為子圈,以南點為中點的半個圓弧,稱為午圈。在地平坐標系中,子圈所起的作用相當於本初子午線在地理坐標系中的作用,是地平經度(方位)度量的起始面。
方位即地平經度,是一種兩面角,即子圈所在的平面與通過天體所在的地平經圈平面的夾角,以子圈所在的平面為起始面,按順時針方向度量。方位的度量亦可在地平圈上進行,以北點為起算點,由北點開始按順時針方向(地平坐標系是左旋坐標系,即用左右向右旋轉握手的方向)計量。方位的大小變化範圍為0°~360°,北點為0°,東點為90°,南點為180°,西點為270°。
方位在地理學和天文觀測中有著廣泛的應用。例如,在野外地質調查中,經常要測量沉積岩岩層的傾向,即岩層的傾斜方向,它就是用方位來表示的。它是用北點的方向與岩層傾斜方向的夾角表示的。如果,其值介於0°~90°,則岩層向東北傾斜,在90°~180°之間則向東南傾斜,在180°~270°之間則向西南傾斜,在270°~360°之間則向西北傾斜。
在天文觀測中,如果預報或觀測到某一天文現象,發生時的方位(南點為起點)為45°,則表示該天文現象發生於西南方。
我們這裡所說的方位,一般是指天文學中的概念,即南點是它的起點,午圈所在的平面是它的起始面。
高度即地平緯度,它是一種線面角,即天體方向和觀測者的連線與地平圈的夾角。在觀測地,天體的高度就是該天體的仰視角。此時無所謂向下計量的高度;但是,在計算時,則會出現負的高度值,這意味著天體位於地平圈以下,即位於不可見半球。天體的高度可以在地平經圈上度量,從地平圈起算,到天頂為0°~90°,到天底為0°~(-90°)。
地平坐標中的方位,還可以用來測定地物相對於觀測者的方向。
地表各點位置不同,地平坐標系的基本圈(地平圈)和基本點(天頂和天底),也隨之不同。所以,在不同地點同時觀察同一天體,所得到的方位和高度是不相同的;在同一地點,由於地球的自轉,時間的延續,對於同一天體在不同的時刻進行觀測,其方位和高度也是不相同的。所以,地平坐標值是因地因時而不同。隨時間和地點的變化而變化是該坐標系的顯著特徵。例如,太陽剛升起的時刻,其方位較大,高度為0°;到了正午時,太陽位於正南方的天空中,其方位為0°,高度則增到了一天中的最大值;到了太陽落山時刻,其方位和高度又發生了明顯的改變。這就是地平坐標值隨時間的變化,這種變化是地球自轉造成的。
下面分別介紹在不同地點,地平坐標系的變化情況。
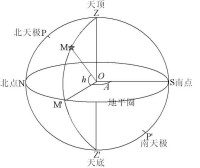
為觀測者在北極的地平坐標系。此時,地平圈與天軸垂直,與地理赤道在天球上投影重合,天北極與天頂重合,天南極與天底重合。因此,天北極的高度就是天頂的高度,其值為90°。
觀測者位於赤道的地平坐標系,在這種情況下,地平圈與天軸位於同一平面,天北極和天南極與天頂、天底的角距離均為90°,地平圈與天赤道垂直,天北極和天南極位於地平圈上。因此,天北極和天南極的高度都是0°。
為觀測者在北半球緯度的地平坐標系。在這裡地平圈與天軸的夾角為0°~90°,這是因為地理緯度為的地平面與地軸的夾角為0°~90°。所以,天北極的高度就是0°~90°,也就是,在北半球的任何一個地點,天北極的高度等於該地的地理緯度。這一規律給我們提供了一種天文測緯的基本方法。只要測量了天極在某地的地平高度,就得出了該地的地理緯度。
地平坐標系能把天體在當時當地的天空位置直觀地、生動地表示出來。例如,若某人造衛星在某時刻的地平坐標值為:方位270°,高度45°,則說明,此時該人造衛星在正西方的天空,其仰角為45°。
在某地連續數小時觀測某一恆星在天空中的位置變化,則可以看出該恆星的高度和方位是隨著時間的推移而變化的。由此,可以對地平坐標系的含義有更清楚的認識。
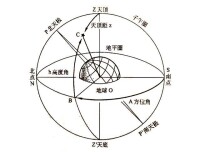
圖1 兩個站心地平坐標系
假設有兩個測站1和2,要將在測站2上測定的點坐標歸入測站1的站心坐標系。設測站1的大地坐標為(BLH) ,測站2的大地坐標為(BLH) ,在測站1、2上測定離散點時,全站儀設置的測站坐標為(UEN) 、(UEN) ,測得點的坐標分別為(UEN) (i=1,2,Λ,m)、(UEN) (i=1,2,Λ,n)。可按下列兩種方法,將在測站2上測定的點的坐標換算為測站1的站心坐標系中的坐標U′E′N′ (i=1,2,Λ,n)。但在實際測量時,一般不能精確知道每個測站的經緯度,但能知道測區大概的經緯度和大地高(BLH) 和近似北方向。可按以下步驟計算每點的經緯度。
1)選一個控制點作為計算基準點,設其經緯度和高程為(BLH) ,按高斯投影正算公式計算該點的高斯坐標,設為(xyH) 。
2)根據各控制點與基準點的坐標差,求得各點的高期坐標(xyH) ,再按高斯投影反算公式計算各點的經緯度(BLH) 。
為確定物體表面的形狀,在不同測站利用全站儀等採集了某物體表面部分點的坐標后,因觀測到的該物體表面的離散點不在同一坐標系中,可以用本文介紹的直接計算修正量或空間直角坐標歸算方法將測定點的坐標歸算到同一個測站的當地切平面坐標系中,然後利用某種合適的曲面擬合的方法進行擬合。本文介紹的不同站心地平坐標系中離散點坐標歸算的方法可以很好的消除不同站心地平坐標系的不平行性給精密測量帶來的誤差,文中所用算例的16個點來自工廠程中一物體表面,要用這些點做曲面擬合,但無法在同一測站觀測到所有點,故設了兩個測站,在其中一個測站可觀測12個點,另一個測站只可觀測到8個點,即有4個公共點,於是應用空間直角坐標換算方法進行坐標歸算,結果在公共點上的觀測坐標和歸算坐標之間最大差異僅有0.0005 m,從而說明該方法在理論上和實際運用中都是嚴密的。在實際的應用中,如果沒有公共點,也可以將已轉換到測站A的站心當地切平面坐標系中的點作為測量值,再歸算到測站B的站心當地切面坐標系中,將其與觀測值之差作為該演演算法的一個檢核標準。