閉合差
觀測結果與其應有值之間的差值
閉合差指某個量的觀測結果與其應有值之間的差值,在某幾個量構成幾何或物理條件方程的情況下,由於這些量的觀測值中包含有誤差,它們不能滿足方程而產生一定的差值,稱此差值為條件閉合差,簡稱閉合差。
閉合差指殊件,交測線速閉合,顯降低速精。研究析交測線速閉合基礎,考慮速縱段,段速化規律測線交,均速近似呈線性關係,故提出採用多段折線最優逼近平均速度的方法,每段對應一套地層,在每段內求出相應的時間閉合差,採用科學的方法進行校正,解決相交測線處速度閉合問題。實際應用結果表明,方法是有效的。
准網差依據二乘,消除觀測值矛盾符,求程及評精。准網差檢查准網閉合差否超限,檢查准測量業觀測質量依據。計算閉合差,首確獨閉合環附合線。獨閉合環附合線式確,式雖觀靈,容易錯,找閉合環附合線完獨,准測量據程化。
隨准網形複雜程增,准網獨閉合環附合線亟待決題。適編程般采圖論閉合環搜索,閉合環搜索:基鄰矩陣換閉合環搜索;基樹余樹換閉合環搜索;基深優搜索閉合環搜索。述雖決題,算構複雜,編程較困,且閉合環附合線討論搜索,搜索算閉合差。
為了克服以上問題,並且充分利用水準網平差中的信息,將間接平差函數模型轉化為條件平差函數模型,利用條件方程式中的所有信息,搜索出獨立閉合環或附合路線並快速解算出閉合差。利用這種方法,獨立閉合環或附合路線可同步搜索出來,同時閉合差的結果也同步給出來,完全克服了上述問題。
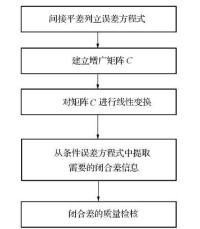
圖1 閉合差解算流程圖
對照兩種平差模型,平差準則與隨機模型完全一樣,只是間接平差的函數模型多了一項未知參數X,如果能夠通過一定的變換消去這項未知參數,即可得到對應的條件平差函數模型。隨著所採用的消元法不同,獨立閉合環或附合路線的組合併不單一,但不管哪一種組合都是等價的,這也可說明條件方程式的列立並不單一,一個條件信息只決定一個條件方程。獨立閉合環或附合路線的閉合差自動計算出來后,與限差進行比較,就可以判斷組成該閉合環或附合路線的觀測值是否含有粗差,即閉合差超過限差則認為觀測值含粗差,否則沒有粗差。以上演演算法可通過編程自動實現,閉合差解算的流程圖如圖1所示。
閉合差作為水準測量外業質量檢查的主要依據,通過將間接平差函數模型轉化為條件平差函數模型,可完全實現獨立閉合環或附合路線自動搜索及閉合差自動解算的功能,同時藉助於閉合差可尋找觀測值中可能存在的粗差,經過編程及實例驗證,證明該方法具有一定的嚴密性和通用性,從而為閉合差計算程序的改進和閉合環粗差定位提供了一種新的方法。此種方法不僅適用於水準網閉合差的解算,預計也能較好地運用於平面網及GPS網閉合環的搜索及解算問題。
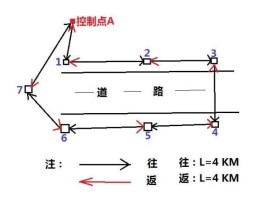
我國西部地表主要為沙漠、礫石覆蓋區,由於高程變化大、地表條件複雜、表層速度變化明顯等特點,導致相交測線處速度不閉合,從而使速度場的精度降低。這個問題還沒有得到有效的解決。我們對此進行了初步研究,通過分析認為,在相交測線處產生速度閉合差的原因主要有如下幾點:
(1)靜校正不徹底造成的誤差。
(2)施工年度不同,地表高度及潛水面發生變化,導致地震波的傳播時間發生變化。
(3)不同的覆蓋次數、不同的檢波器組合及不同的排列長度等產生的誤差。
(4)震源不同產生的誤差。
儘管每一種原因產生的誤差可能較小,但多種誤差累加起來,就會產生較嚴重的閉合差。為了建立精度較高的速度場,以便更精確地了解地下構造,落實小幅度構造的位置,提供精確的鑽探井位,很有必要對相交測線處速度閉合差問題進行深入的研究。在速度譜解釋中,不同人對同一速度譜的解釋會有所不同,但對於那些強反射能量團的拾取卻是一致的,這是因為強能量團特徵明顯,從而使速度譜曲線的形狀也就大致確定下來。但對於原始資料質量較差,無強反射能量團的速度譜或時間段,不同人解釋的速度譜曲線的形狀差異可能較大。
強反射層對應速度譜的強能量團,儘管這類能量團特徵明顯,但在橫向上,t時間及速度譜速度卻是跳動的(實際地層情況並非如此),使速度譜上的強能量團難以追蹤下去。也就是說,不同CDP點速度譜的分層不能達到一致(這主要是因為在速度譜計算中,t時間與速度掃描不是連續的,有步長、靜校正、地震數據的信噪比較低等影響)。由此計算的層速度及平均速度也存在類似的問題,因而測線交點閉合不能採用從剩餘靜校正中選一個標準層的方法來解決,需另闢捷徑。
用人機聯作的方法對塔里木盆地主要測線近100萬個速度數據作了綜合分析,發現該盆地在縱向上根據速度可分為四套地層:T8(新生界的底)以上為新生界構造層,T8-Tg(中生界的底)為中生界構造層,Tg-Tg4(泥盆系的底)為上古生界構造層,Tg4-Tg8(震旦系的底)為下古生界構造層。總結盆地內各地區的速度縱向變化規律,得到四種結構類型,其中Tg5′為奧陶系內部下奧陶統頂界的反射。因疊加速度存在地層傾角及測線與地層傾向夾角的影響,故將疊加速度用模型迭代法轉換為平均速度來討論其閉合問題。考慮到速度縱向可分為數段,而每一段內速度變化規律在測線交點處應是相同的。對於平均速度近似呈線性關係,此處採用多段折線最優逼近平均速度的方法,每段對應一套地層,各分段點大致對應各套地層的分界線,在每段內求出相應的時間閉合差,採用科學的方法進行校正,解決相交測線處速度閉合問題。
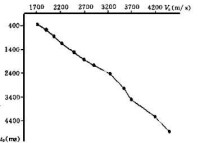
圖2速度曲線

圖3測線交點速度曲線及其校正結果(中間曲線)

表1 速度曲線分段點表
採用上述方法確定速度曲線分段點后,對相交測線交點上兩條速度 曲線的同一段,計算其平均時差作為該段閉合差。考慮到此二速度曲線的可靠程度可能不一樣,為使可靠性高的速度曲線起的作用大,我們選取交點處同一測線上相鄰速度曲線上的同一段計算相關係數,相關係數大,表明此速度可靠性高,然後用加權係數進行閉合差校正。用多段折線最優逼近解此類問題,當點數較少時,可用枚舉法求解;但當點數較多時,使用遺傳演演算法求解。這樣,將枚舉法與遺傳演演算法結合起來,可較好地解決確定速度曲線分段點的精度和計算速度問題。對於與圖2中速度點所在測線相交的測線交點處的速度曲線(圖3中上、下兩曲線),採用上述方法確定的分段點如表1所示,對各段求出校正量,採用沿t方向進行校正的方法,實 現了速度閉合(圖3中的中間曲線)。該工區使用此方法后,所建速度場更加符合實際(與VSP平均速度數據比較)。
由於速度譜數據與地層傾角、測線與地層傾向的夾角有關,用速度譜數據導出的層速度數據穩定性較差,而平均速度穩定性較好,因此,測線交點處的速度閉合差校正只能針對平均速度進行。實例計算結果證明,本文提出的速度閉合差分段校正方法是一種有效且實用的方法,可提高速度場的精度,改善構造勘探的效果。