弧度
平面角的一種量度單位
在數學和物理中,弧度是指平面角的一種量度單位,它是由國際單位制導出的單位,單位縮寫是rad。弧長等於半徑的弧,其所對的圓心角為1弧度(即兩條射線從圓心向圓周射出,形成一個夾角和夾角正對的一段弧。當這段弧長正好等於圓的半徑時,兩條射線的夾角的弧度為1)。弧度大小等於角所對的弧長被半徑除的商,1弧度等於180°/π=57.3°。
根據定義,一周的弧度數為2πr/r=2π,360°角=2π弧度,因此,1弧度約為57.3°,即57°17'44.806'',1°為π/180弧度,近似值為0.01745弧度,周角為2π弧度,平角(即180°角)為π弧度,直角為π/2弧度。
在具體計算中,角度以弧度給出時,通常不寫弧度單位,直接寫值。最典型的例子是三角函數,如sin 8π、tan (3π/2)。
在初中數學中,我們學過圓弧長公式:
弧長=nπr/180,在這裡n就是角度數,即圓心角n所對應的弧長。
但如果我們利用弧度的話,以上的式子將會變得更簡單:(注意,弧度有正負之分)
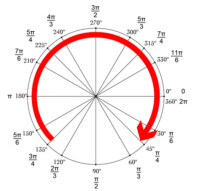
弧度
同樣,我們可以簡化扇形面積公式:
S=|α| r^2/2(二分之一倍的α角的大小,與半徑的平方之積,從中我們可以看出,當|α|=2π,即周角時,公式變成了S=πr^2,圓面積的公式!)
在 Windows 操作系統附帶的計算器程序(電腦左下角的開始→程序→附件→計算器)的科學計演演算法里,可以調用弧度來進行計算。
| 度 | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| 弧度 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 3π/2 | 2π |