截面慣性矩
衡量截面抗彎能力的幾何參數
截面慣性矩指截面各微元面積與各微元至截面上某一指定軸線距離二次方乘積的積分。截面慣性矩是衡量截面抗彎能力的一個幾何參數。任意截面圖形內取微面積dA與其搭配z軸的距離y的平方的乘積y²dA定義為微面積對z軸的慣性矩,在整個圖形範圍內的積分則稱為此截面對z軸的慣性矩Iz。
截面各微元面積與各微元至截面上某一指定軸線距離二次方乘積的積分。慣性矩平移公式: Iz=Ix+Ad^2 這裡, Iz是對於 z-軸的面積慣性矩、 Ix是對於平面質心軸的面積慣性矩、 A是面積、 d是 z-軸與質心軸的垂直距離。(單位:mm^4)
截面各微元面積與各微元至截面上某一指定軸線距離二次方乘積的 積分。
截面慣性矩是衡量截面抗彎能力的一個幾何參數。任意截面圖形內取微面積dA與其搭配z軸的距離y的平方的乘積y2dA定義為微面積對z軸的慣性矩,在整個圖形範圍內的積分則稱為此截面對z軸的慣性矩Iz。慣性矩平移公式:
Iy總=∫z總^2dA=∫(z+b)^2dA=∫z^2dA+2b∫zdA+b^2A=Iy+b^2A
其中:“Iy總”表示在y1Oz1坐標系下的慣性矩,而Iy指在yoz下的慣性矩
Iz總=∫y總^2dA=∫(y+b)^2dA=∫y^2dA+2b∫ydA+b^2A=Iz+b^2A
其中:“Iz總”表示在y1Oz1坐標系下的慣性矩,而Iz指在yoz下的慣性矩
常見截面的慣性矩公式
b*h*h*h/12 其中:b—寬;h—高
b*h*h*h/36 其中:b—底長;h—高
π*d*d*d*d/64 其中:d—直徑
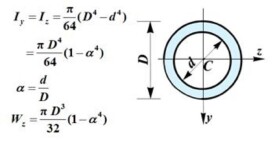
π*D*D*D*D*(1-α*α*α*α)/64; α=d/D 其中:d—內環直徑;D—外環直徑
I=質量X垂直軸二次)the moment of inertia
characterize an object's angular acceleration due to torque.
靜矩(面積X面內軸一次)
把微元面積與各微元至截面上指定軸線距離乘積的積分稱為截面的對指定軸的靜矩Sx= ydF。
截面慣性矩
截面慣性矩:the area moment of inertia
characterized an object's ability to resist bending and is required to calculate displacement.
截面各微元面積與各微元至截面某一指定軸線距離二次方乘積的積分Ix= y↑2dF。
截面極慣性矩(Ip=面積X垂直軸二次)。
Ip: the torsional moment of inertia
the polar moment of inertia
截面各微元面積與各微元至垂直於截面的某一指定軸線二次方乘積的積分Ip= P↑2dF。
a quantity to predict an object's ability to resist torsion, to calculate the angular displacement of an object subjected to a torque.
截面慣性矩和極慣性矩的關係
截面對任意一對互相垂直軸的慣性矩之和,等於截面對該二軸交點的極慣性矩Ip=Iy+Iz。
section factor
根據材料力學,在承受彎矩Μ的梁截面上和承受扭矩T 的桿截面上,最大的彎曲應力σ和最大的扭轉應力τ出現於離彎曲中性軸線和扭轉中性點垂直距離最遠的面或點上。σ和τ的數值為 -0.032√(C+W)-0.21√(RD↑2) 式中Jxx和J0分別為圍繞中性軸線XX和中性點O的截面慣性矩;Jxx/y和J0/y分別為彎曲和扭轉的截面模量(見圖和附表)。一般截面係數的符號為W,單位為毫米3 。依據公式可知,截面的抗彎和抗扭強度與相應的截面係數成正比。
迴轉半徑又稱慣性半徑I
迴轉半徑是指物體微分質量假設的集中點到轉動軸間的距離,它的大小等於轉動慣量除總質量后再開平方。