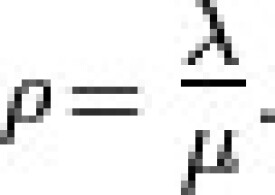m/m/1

這種模型是一種出生-死亡過程，此隨機過程中的每一個狀態代表模型中人數的數目。因為模型的隊列長度無限且參與人數亦無限，故此狀態數目亦為無限。例如狀態0表示模型閑置、狀態1表示模型有一人在接受服務、狀態2表示模型有二人（一人正接受服務、一人在等候），如此類推。此模型中，出生率（即加入隊列的速率）λ在各狀態中均相同，死亡率（即完成服務離開隊列的速率）μ亦在各狀態中相同（除了狀態0，因其不可能有人離開隊列）。故此，在任何狀態下，只有兩種事情可能發生：

有人加入隊列。如果模型在狀態k，它會以速率λ進入狀態

有人離開隊列。如果模型在狀態k（k不等於0），它會以速率μ進入狀態

由此可見，模型的隱定條件為。如果死亡率小於出生率，則隊列中的平均人數為無限大，故此這種系統沒有平衡點。

λ：平均到達的顧客數（單位時間平均到達率，個/秒）

μ：平均服務的顧客數（服務率、離開率，個/秒），每客平均服務時間 ,

:平均等待隊列長度（在隊列中排隊等待的顧客數）

:每個顧客的平均等待時間，包括沒有排隊的顧客

L：系統中平均顧客數=正在被服務的顧客數+正在等待的顧客數

W：平均等待時間=平均等待時間+平均服務時間

ρ:平均利用率，一段相當長的時間內可測得

定義

則模型在狀態的機率為

由此，可給出各測量數值的公式：

整個系統的平均人數： ，且其變異（variance）為：（方差）

一單位時間內系統完成服務的人數：

在隊列中等候服務的人數：

一人在系統中的平均逗留（等候+接受服務）時間：

一人的平均等候時間：

系統中有n個顧客的概率,它決定了系統運行的特徵。穩定情況下，與t無關，; 狀態轉移平衡方程：轉入率=轉出率；狀態i轉移到狀態的轉移率λiPi; 狀態轉移到狀態i的轉移率; 狀態平衡方程：

1

2

.... ....................... ...................

N -1

N .... ...................

狀態：0:

狀態：1:

狀態：n-1:

狀態：n :

，則

為變隊長極其概率的積之和或者

(第n個顧客到來時的對長為,發生概率） 或者

可用M/M/1模型的例子眾多，例如只有一位員工的郵局，只有一隊列。客人進來，排隊、接受服務、離開。如果客人進來的數目符合 泊松過程，且服務時間是 指數分佈，則可用M/M/1模擬，並算出平均隊列長度、不同等候時間的機率等。

M/M/1可一般化成為M/M/n模型，使可用時接受服務的人數為大於一。歷史上，M/M/n模型首先被用來模擬電話系統，因為荷蘭工程師Erlang發現客人打電話的速率符合 泊松過程，且通話時間是 指數分佈，所以佔用通訊線路的數目和等待接線的人數符合M/M/n模型。