空間直角坐標系
數學概念之一
與空間解析幾何相似,為了確定空間中任意一點的位置,需要在空間中引進坐標系,最常用的坐標系是空間直角坐標系。
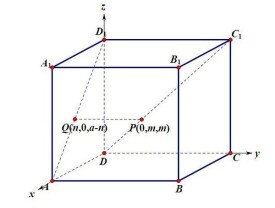
空間任意選定一點O,過點O作三條互相垂直的數軸Ox,Oy,Oz,它們都以O為原點且具有相同的長度單位。這三條軸分別稱作x軸(橫軸),y軸(縱軸),z軸(豎軸),統稱為坐標軸。它們的正方向符合右手規則,即以右手握住z軸,當右手的四個手指x軸的正向以角度轉向y軸正向時,大拇指的指向就是z軸的正向。這樣就構成了一個空間直角坐標系,稱為空間直角坐標系O-xyz。定點O稱為該坐標系的原點。與之相對應的是左手空間直角坐標系。一般在數學中更常用右手空間直角坐標系,在其他學科方面因應用方便而異。
任意兩條坐標軸確定一個平面,這樣可確定三個互相垂直的平面,統稱為坐標面。其中x軸與y軸所確定的坐標面稱為xOy面,類似地有yOz面和zOx面。三個坐標面把空間分成八個部分,每一部分稱為一個卦限。如右圖所示,八個卦限分別用字母Ⅰ、Ⅱ、...、Ⅷ表示,其中含x軸、y軸和z軸正半軸的是第Ⅰ卦限,在xOy面上的其他三個卦限按逆時針方向排定,依次為第Ⅱ、Ⅲ、Ⅳ卦限;在xOy面下方與第Ⅰ卦限相鄰的為第Ⅴ卦限,然後也按逆時針方向排定依次為第Ⅵ、Ⅶ、Ⅷ卦限。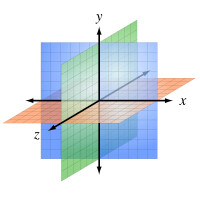

空間直角坐標系
設點M為空間的一點,過點M分別作垂直於x軸、y軸和z軸的平面。設三個平面與x軸、y軸和z軸的交點依次為P、Q、R,點P、Q、R分別稱為點M在x軸、y軸和z軸上的投影。又設點P、Q、R在x軸、y軸和z軸上的坐標依次為x、y、z,於是點M確定了一個有序數組x,y,z。反之,如果給定一個有序數組x,y,z,可以在x軸上取坐標為x的點P,在y軸上取坐標為y的點Q,在z軸上取坐標為z的點R,然後點P、Q、R分別作垂直於x軸、y軸和z軸的三個平面,它們相交於空間的一點M,點M就是由有序數組x,y,z所確定的點。這樣一來,空間的點M與有序數組x,y,z之間就建立了一一對應的關係。把有序數組x,y,z稱為點M的坐標,記作M(x,y,z),其中x稱為橫坐標、y稱為縱坐標、z稱為豎坐標。
原點的坐標為(0,0,0);若點M在x軸上,則其坐標為(x,0,0);同樣對於y軸上的點,其坐標是(0,y,0);對於z軸上的點,其坐標為(0,0,z);同樣,位於xOy平面上的點,其坐標為(x,y,0);位於yOz平面上的點,其坐標為(0,y,z);位於xOz平面上的點,其坐標為(x,0,z)。可見,位於坐標軸上、坐標面上和各卦限內的點,其坐標各有特點。
利用點的坐標,可求出空間中兩點間的距離。
設A(x1,y1,z1)和B(x2,y2,z2)是空間兩點,過A和B各作三個分別垂直於坐標軸的平面,這六個平面圍成一個以AB為對角線的長方體,它的三條棱長分別是,由於A和B之間的距離d就是該長方體對角線AB的長度,且和都是直角三角形,故由勾股定理得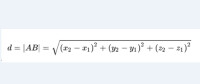
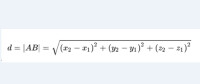
空間直角坐標系
這就是空間兩點間的距離公式。
特殊地,空間的點M(x,y,z)與原點O(x,y,z)之間的距離為
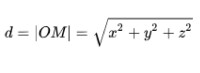
空間直角坐標系