共找到2條詞條名為晶面指數的結果 展開
- 地質學術語之一
- 密勒指數
晶面指數
地質學術語之一
晶面指數是晶體的常數之一,通過空間點陣中任意三個結點的平面稱為晶面。
是晶面在3個結晶軸上的截距係數的倒數比,當化為整數比后,所得出的3個整數稱為該晶面的米勒指數(Miller index)。六方和三方晶系晶體當選取4個結晶軸時,一個晶面便有4個截距係數,由它們的倒數比所得出的4個整數則稱為晶面的米勒—布拉維指數(Miller Bravais indices)。以上兩種指數一般通稱為晶面指數。
通過空間點陣中任意三結點的平面稱為晶面。點陣中一定有一系列間距相等的晶面與此晶面相平行,為表徵晶面,採用晶面指數,亦稱為米勒(M.H.Miller)指數。只要求得任一晶面與三條晶軸的三個截距.取其倒數,用最小公倍數乘之,將所得最小(互質)整數加以圓括弧,即為晶面指數(若截距為負值,需在晶面指數上加一負號)。
● ● 1.對晶胞作晶軸X、Y、Z,以晶胞的邊長作為晶軸上的單位長度;
● ● 2.求出待定晶面在三個晶軸上的截距(如該晶面與某軸平行,則截距為∞),例如 l、1、∞,1、1、1,1、1、1/2等;
● ● 3.取這些截距數的倒數,例如 110,111,112等;
● ● 4.將上述倒數化為最小的簡單整數,並加上圓括弧,即表示該晶面的指數,一般記為(hkl),例如(110),(111),(112)等。
● ● 下面再舉例來加以說明:
● ● 圖1-17中所標出的晶面a1b1c1,相應的截距為1/2、1/3、2/3,其倒數為2、3、3/2,化為簡單整數為 4、6、3,所以晶面a1b1c1的晶面指數為(463)。圖1-18表示了晶體中一些晶面的晶面指數。
● ● 圖1-17晶面指數的表示方法
● ● 圖1-18 幾個晶面的晶面指數
● ● 圖1-19 {100},{111},{110} 晶面族
● ● 對晶面指數需作如下說明:h、k、l分別與X、Y、Z軸相對應,不能隨意更換其次序。若某一數為 0,則表示晶面與該數所對應的坐標軸是平行的。例如(h0l)表明該晶面與Y軸平行。若截某一軸為負方向截距,則在其相應指數上冠以“-”號,如(hk)、(kl)等。在晶體中任何一個晶面總是按一定周期重複出現的,它的數目可以無限多,且互相平行,故均可用同一晶面指數(hkl)表示。所以(hkl)並非只表示一個晶面,而是代表相互平行的一組晶面。 h、k、l分別表示沿三個坐標軸單位長度範圍內所包含的該晶面的個數,即晶面的線密度。例如,(123)表示在X軸的單位長度內有 1個該晶面,在Y軸單位長度內有 2個該晶面,而在 Z軸單位長度內有 3個該晶面,而其中距原點最近的晶面在三坐標軸上的截距為1、1/2、1/3。在晶體中有些晶面具有共同的特點,其上原子排列和分佈規律是完全相同的,晶面間距也相同,唯一不同的是晶面在空間的位向,這樣的一組等同晶面稱為一個晶面族,用符號{hkl}表示。在立方系中,晶面族中所包含的各晶面其晶面指數的數字相同,但數字的排列次序和正負號不同。例如圖1-19所示,在立方系中:
● ● {100}包括(100)、(010)、(001);
● ● {110}包括(110)、(101)、(011)、(1-10)、(10-1)、(01-1);
● ● {111}包括(111)、(11-1)、(-111)、(1-11)。
● ● 而{123}則包括(123)、(132)、(231)、(213)、(312)、(321);
● ● (-123)、(-132)、(-231)、(-213)、(-312)、(-321);
● ● (1-23)、(1-32)、(2-31)、(2-13)、(3-12)、(3-21);
● ● (12-3)、(13-2)、(23-1)、(21-3)、(31-2)、(32-1)。
● ● 共24組晶面。
● ● 在立方晶系中,具有相同指數的晶向和晶面必定是相垂直的,即[hkl] 垂直於(hkl)。例如:[100] 垂直於(100),[110] 垂直於(110),[111] 垂直於(111),等等。但是,此關係不適用於其它關係。
晶面指數實質上反映了晶面法線在點陣中的取向,亦即晶面上結點的分佈特徵。顯然,單位晶面的晶面指數為(1 1 1),凡晶面平行於某一坐標軸(如X軸)者,其晶面指數具有的形式( 0 k l ),而晶面同時平行於二條坐標軸(如Y軸和X軸)者,其晶面指數則具有( 0 0 l )的形式。
固態物質按其原子(或分子)的聚集狀態可分為兩大類:晶體與非晶體。
在晶體中,原子(或分子)在三維空間作有規則的周期性重複排列。而非晶體就不具有這一特點,原子雖然處於緊密聚集的狀態,但不存在長程的周期性排列。從液態到非晶態固體的轉變是逐漸過渡的,沒有明顯的凝固點(反之亦然,無明顯的熔點)。而液體轉變為晶體則是突變的,有一定的凝固點和熔點。
非晶體的另一特點是沿任何方向測定其性能所得結果都是一致的,不因方向而異,稱為各向同性或等向性。晶體就不是這樣,沿著一個晶體的不同方向所測得的性能並不相同(如導電性、導熱性、熱膨脹性、彈性、強度、光學數據以及外表面的化學性質等等),晶體的異向性是因其原子的規則排列而造成的。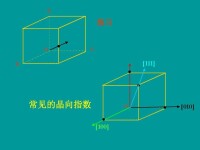

晶面指數
非晶體在一定條件下可轉化為晶體。例如,玻璃經高溫長時間加熱后能形成品態玻璃;而通常呈晶體的物質如果將它從液態快速冷卻或採用一些特殊的製備方法可能得到非晶體。
位於同一直線上的陣點,每隔一個相等的距離就重複出現。同樣,位於同一平面上的陣點構成了二維的點陣平面,將點陣平面沿一定方向平移一定距離,其陣點亦具有重複性。總之,由於各陣點的周圍環境相同,空間點陣具有周期重複性。
因此,為了說明點陣排列的規律和特點,可在點陣中取出一個具有代表性的基本單元(通常是取一個最小的平行六面體)作為點陣的組成單元,稱為晶胞。
晶體中任意兩節點間連線所指的方向稱為晶向。它和通過坐標原點的平行矢量的方向一致,常用符號[ u v w ]表示。u 、v、 w是平行矢量上任意一點在x,y,z坐標上坐標位置的最小整數比。
例如:[ 2 1 0 ]晶向就可視為從坐標原點到坐標(2,1,0)點連線的方向。
點陣中尚有許多方位不同、但面間距均相等(面上結點分佈規律相同)的一些晶面組,可歸併為一個晶面族,記為{ 0 k l}。
例如,在立方晶系中,{1 0 0}族有六個(1 0 0)組,{1 1 1}族有八個(1 1 1)組,{1 1 0}族有十二個(1 1 0)組。
