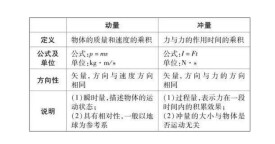
衝量與動量

由,設可得

即可說：物體所受合外力的衝量就是該物體的動量變化量.

衝量是描述力對物體作用的時間累積效應的物理量。力的衝量是一個過程量。在談及衝量時，必須明確是哪個力在哪段時間上的衝量。

例：質量為3千克的甲、乙兩物體，甲物體以初速10米/秒自30米高處斜向上拋出，乙物體自足夠大的光滑曲面無初速下滑，試比較甲、乙兩物體2秒內所受重力衝量的大小。

分析和解：重力是恆力，故重力在2秒內的衝量牛。秒牛。秒，方向豎直向下。

重力的衝量只與重力的大小和作用時間有關，與物體做什麼運動，是否受其它力無關。因此甲、乙兩物體2秒內所受重力衝量相等。

又如 質量為3千克的物體，以2米/秒的速度沿水平光滑地面向東運動。物體受到一個向東的4牛的力的作用6秒，接著這個力變為向西5牛，作用4秒。求這個力在10秒內的衝量。

解 取向東方向為正方向，力F在前6秒內的衝量為牛。。秒。力F在後4秒內的衝量為牛。牛。秒。所以，力F在10秒內的衝量為牛。秒。正號說明衝量方向向東。

衝量是矢量，在計算時一定要注意建立坐標。

質點的質量m與其速度v的乘積（mv）。動量是矢量，用符號p表示。質點組的動量為組內各質點動量的矢量和。物體的機械運動都不是孤立地發生的，它與周圍物體間存在著相互作用，這種相互作用表現為運動物體與周圍物體間發生著機械運動的傳遞（或轉移）過程，動量正是從機械運動傳遞這個角度度量機械運動的物理量，這種傳遞是等量地進行的，物體2把多少機械運動（動量）傳遞給物體1，物體2將失去等量的動量，傳遞的結果是兩者的總動量保持不變。從動力學角度看，力反映了動量傳遞快慢的情況。與實物一樣，電磁場也具有動量。例如光子的動量為，其中h為普朗克常量，k為波失，其大小為（λ 為波長），方向沿波傳播方向。在國際單位制中，動量的單位為千克·米/秒（kg·m/s）。

一般而言，一個物體的動量指的是這個物體在它運動方向上保持運動的趨勢。動量實際上是牛頓第一定律的一個推論。

動量是一個守恆量，這表示為在一個封閉系統內動量的總和不可改變。

動量守恆定律是最早發現的一條守恆定律，它起源於16～17世紀西歐的哲學家們對宇宙運動的哲學思考。

觀察周圍運動著的物體，我們看到它們中的大多數，例如跳動的皮球、飛行的子彈、走動的時鐘、運轉的機器，都會停下來。看來宇宙間運動的總量似乎在減少。整個宇宙是不是也像一架機器那樣，總有一天會停下來呢？但是，千百年來對天體運動的觀測，並沒有發現宇宙運動有減少的跡象。生活在16、17世紀的許多哲學家認為，宇宙間運動的總量是不會減少的，只要能找到一個合適的物理量來量度運動，就會看到運動的總量是守恆的。這個合適的物理量到底是什麼呢?

法國哲學家兼數學家、物理學家笛卡兒提出，質量和速率的乘積是一個合適的物理量。可是後來，荷蘭數學家、物理學家惠更斯(1629—1695)在研究碰撞問題時發現：按照笛卡兒的定義，兩個物體運動的總量在碰撞前後不一定守恆。

牛頓在總結這些人工作的基礎上，把笛卡兒的定義作了重要的修改，即不用質量和速率的乘積，而用質量和速度的乘積，這樣就找到了量度運動的合適的物理量。牛頓把它叫做“運動量”，1687年，牛頓在他的《自然哲學的數學原理》一書中指出：某一方向的運動的總和減去相反方向的運動的總和所得的運動量，不因物體間的相互作用而發生變化；還指出了兩個或兩個以上相互作用的物體的共同重心的運動狀態，也不因這些物體間的相互作用而改變，總是保持靜止或做勻速直線運動。

2.動量守恆定律的適用範圍比牛頓運動定律更廣

近代的科學實驗和理論分析都表明：在自然界中，大到天體間的相互作用，小到如質子、中子等基本粒子間的相互作用，都遵守動量守恆定律。因此，它是自然界中最重要、最普遍的客觀規律之一，比牛頓運動定律的適用範圍更廣。下面舉一個牛頓運動定律不適用而動量守恆定律適用的例子。

在我們考察光的發射和吸收時，會看到這樣一種現象：在宇宙空間中某個地方有時會突然發出非常明亮的光，這就是超新星。可是它很快就逐漸暗淡下來。光從這樣一顆超新星出發到達地球需要幾百萬年，而相比之下超新星從發光到熄滅的時間就顯得太短了。

當光從超新星到達地球時，它給地球一個輕微的推動，而與此同時地球卻無法給超新星一個輕微的推動，因為它已經消失了。因此，如果我們想像一下地球與超新星之間的相互作用，在同一瞬間就不是大小相等、方向相反了。這時，牛頓第三定律顯然已不適用了。

雖然如此，動量守恆定律還是正確的。不過，我們必須把光也考慮在內。當超新星發射光時，星體反衝，得到動量，同時光也帶走了大小相等而方向相反的動量。等經過幾百萬年之後光到達地球時，光把它的動量傳給了地球。這裡要注意的是：動量不僅可以為實物所攜帶，而且可以隨著光輻射一起傳播。當我們考慮到上述這點時，動量守恆定律還是正確的。

p：動量（kg·m/s） m：質量（kg） v：速度（m/s）

無論哪一種形式的碰撞，碰撞前後兩個物體mv的矢量和保持不變.

由於速度是矢量，所以動量也是矢量，它的方向與速度的方向相同.

(1)I=Ft中的F為恆力，也可理解為方向不變的變力在時間t內的平均力F。如果力的大小、方向都是變化的，則不能用Ft表述其衝量，變力的衝量在一定條件下可用質點動量的變化間接表述。

(2)衝量是矢量，求衝量不僅要求大小，還要求方向、恆力衝量的方向與恆力同向，變力衝量的方向與動量的變化量方向一致。

(3)衝量是過程量。論及衝量時要明確是哪個力或哪幾個力在哪一段時間內的衝量。

(4)衝量大小隻決定於力和力所作用的時間，而與物體是否受其它力及物體的運動狀態無關。

動量，是表示質點機械運動狀態的物理量，是瞬時量。

動量變化量定義為

動量是矢量，在計算動量變化時，一定要注意坐標的選取。

1.放在水平桌面上的質量為m的物體，用一個FN的水平推力推它ts，物體始終保持靜止，則力FN的衝量是_______ N·s，合力的衝量是_______；.

2.如下圖標準跑道上，某運動員以大小為6m/s的速度勻速前進，此運動員質量為55kg，當他跑到最南端時動量大小為 _______，方向 _______；當他跑到最東端時，動量大小為_______ ，方向 _______；從最南端到東端過程中，動量的改變數為______ ，方向 ________；從最南端到最北端過程中，動量的改變數為_______，方向_______。

3.下列說法中正確的是( )

A.物體的質量越大，其動量就越大

B.受力大的物體，受到的衝量就一定大

C.物體動量改變速率一定改變

D.物體動量改變了，但物體的速率可以不變

4.如下圖，兩個質量相等的物體在同一高度沿傾角不同的兩個光滑斜面由靜止自由滑下，到達斜面底端的過程中，兩物體具有相同的物理量是( )

A.重力的衝量 B.彈力的衝量

C.到達的底端時的動量 D.以上幾個量都不是

5.有一質量為M的物體，沿一傾角為θ的光滑斜面由靜止自由滑下，斜面長為L，則物體到達斜面底端的過程中，重力的衝量大小為___ ，方向___ ；彈力的衝量大小為____ ，方向___ ；合外力的衝量大小為 ____，方向____ .

6.質量為150g的皮球從離地5m處自由落下，它在第1s內動量變化大小為 方向；若皮球觸地后反彈到離地3.2m處時速度要變為零，皮球與地碰撞過程中動量變化的大小為 ___，方向___ .(g取10m/s2)

7.在地面上以豎直向上的初速度υ0拋出一個質量為m的物體，物體從拋出到落地過程中動量的變化大小_____，方向____ ；物體在全部運動過程中受到的衝量大小____，方向_____ .

8.以水平初速度10m/s平拋一個質量為100g的小球，求(1)2s內小球動量變化的大小和方向；(2)2s內重力的衝量.

1. F·t；0；

2. ，正東；，正北；，正西 北；，正西；

3.D；4.D；

5.，豎直向下；mcosθ垂直斜面向上；m沿斜面向下；

6. ，豎直向下；，豎直向上。

7. 豎直向下；，垂直向下，8.，豎直向下； ，豎直向下。