共找到2條詞條名為凸性的結果 展開
- 史樹中著圖書
- 曲線凹或凸的統稱
凸性
曲線凹或凸的統稱
凸性是數學術語。曲線的凹或凸統稱為曲線的凸性。只要知道了函數的凸性即找到函數的凹凸區間,拐點就顯而易得。
科
切線角講,凸弧切線曲線弧,凸弧切線曲線弧。
割線角度講,如果連續曲線y=f(x)在區間(a,b)對應的曲線弧上任意兩點的割線線段都在該兩點間的曲線弧之上,則稱該段曲線弧是下凸的,並稱函數y=f(x)在區間(a,b)上是下凸的(或上凹的,即曲線開口向上)。如果連續曲線y=f(x)在區間(a,b)對應的曲線弧上任意兩點的割線線段都在該兩點間的曲線弧之下,則稱該段曲線弧是上凸的,並稱函數y=f(x)在區間(a,b)上是上凸的(或下凹的,即曲線開口向下)。
從導數角度講,設y=f(x)在(a,b)內具有二階導數,如果在(a,b)內f''(x)>o,則y=f(x)在(a,b)內為下凸;如果在(a,b)內f''(x)。
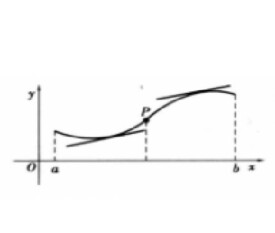
在研究函數圖形的變化時,僅僅研究單調性並不能完全反映它的變化規律。如圖1,函數雖然在區間[a,b]內單調遞增,但卻有不同的彎曲狀況,從左到右,曲線先是向下凹,通過P點后改變了彎曲方向,曲線向上凸。因此,在研究函數的圖形時,除了研究其單調性,對於它的彎曲方向及彎曲方向的改變點的研究也是很有必要的。從圖1明顯可知,曲線向下凹時,彎曲的弧段位於這弧段上任意一點的切線的上方,曲線向上凸時,彎曲的弧段位於這弧段上任意一點的切線的下方。
凹函數和凸函數
如果在某區間I內,連續函數 的曲線弧位於其上任意一點切線的上方(下方),則稱曲線在這個區間內是凹的(凸的),區間I稱為函數 的凹區間(凸區間),記為 ,函數 則為區間I上的凹函數(凸函數)。
凸性的定義
連續曲線上,凹曲線和凸曲線的分界點稱為曲線的拐點。
曲線的凹或凸統稱為曲線的凸性,顯然,只要知道了函數的凸性即找到函數的凹凸區間,拐點就顯而易得。
設函數 在區間[a,b]上連續,在(a,b)內具有二階導數,則:
①如果 時,恆有 ,則曲線 在[a,b]內是凹的;
②如果 時,恆有 ,則曲線 在[a,b]內是凸的。
因為 時, 單調增加,即斜率 由小變大,曲線是凹的,如圖2、3所示;反之,如果 時, 單調減少,即斜率 由大變小,曲線是凸的,如圖4、5所示。
拐點既然是曲線上凸凹的分界點,故在拐點的左右鄰域 必然異號,而拐點處的二階導數 或 不存在,因此在確定拐點時,首先找到 或 不存在的點,以這些點將定義域劃分為若干個子區間,然後檢驗這些點左右鄰域 的符號,若異號則為拐點,否則不是拐點。
例1 求曲線 的凹凸區間與拐點。
解: 易知,定義域為(-∞,+∞),求導數得
令 ,得 ,且二階導數沒有不存在的點。
以 為分界點,將定義域劃分為3個子區間,並討論函數在各子區間上的凸性及拐點,見表1。
| 表1 | |||||
| x | (-∞,0) | (0,1) | 1 | (1,+∞) | |
| y'' | + | - | + | ||
| y | ∪ | 拐點 | ∩ | 拐點 | ∪ |
從表1可知,該曲線的凹區間為(一∞,0),(1,+∞),凸區間為(0,1);曲線的拐點為(0,1)和(1,0)。
例2 求曲線 的凹凸區間及拐點。
解: 易知,定義域為(-∞,+∞),求導數得
由二階導數可知,無 的點;當 時, 不存在.見表2。
| 表2 | |||
| x | (-∞,2) | 2 | (2,+∞) |
| y'' | - | 不存在 | + |
| y | ∩ | 拐點 | ∪ |
由表2知,曲線的凹區間為(2,+∞),凸區間為(-∞,2);拐點為(2,0)。