高分子溶液(macromolecular solution)是膠體的一種,在合適的介質中高分子化合物能以分子狀態自動分散成均勻的溶液,分子的直徑達膠粒大小。

高分子溶液
高分子溶液(macromolecular solution/polymer solution)是一種在合適的介質中高分子化合物能以分子狀態自動分散成均勻的溶液的膠體,分子的直徑達膠粒大小。高分子溶液的本質是真溶液,屬於均相分散系。高分子溶液的黏度和
滲透壓較大,分散相與分散系親和力強,但
丁達爾(Tyndall)現象不明顯,加入少量電解質無影響,加入多時引起
鹽析。
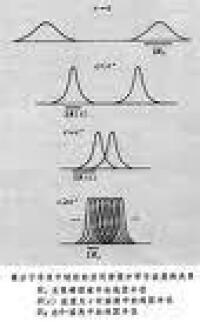
高分子溶液
高分子化合物在形成溶液時,與低分子量的物質明顯不同的是要經過溶脹(swelling)的過程,即溶劑分子慢慢進入捲曲成團的高分子化合物分子鏈空隙中去,導致高分子化合物舒展開來,體積成倍甚至數十倍的增長。不少高分子化合物與水分子有很強的親和力,分子周圍形成一層水合膜,這是高分子化合物溶液具有穩定性的主要原因。因此高分子溶液是穩定系統。

高分子溶液
指高聚物溶解在溶劑中形成的溶液。在高分子科學發展的早期,由於溶液中高分子的尺寸大小與膠體粒子的大小相似,因此高分子溶液曾一度被錯誤地認為是一種膠體溶液,後來很多實驗證明高分子溶液是處在
熱力學平衡狀態的真溶液,而且是能用熱力學函數來描述的分子分散的穩定體系。研究高分子稀溶液的性質可以得到高分子的分子量與分子量 分佈、高分子在溶液中的形態和尺寸大小以及高分子與溶劑分子間相互作用等重要參數。高分子的極稀溶液的減阻作用在
流體力學方面得到實際應用。
高分子濃溶液在合成纖維生產中的溶液紡絲、干法紡絲,片基生產中的溶液鑄膜,塑料的增塑等都有密切的關係。這方面的研究側重在高分子溶液的流變性能與成型工藝的關係。高分子溶液的混合熱、混合熵和混合自由能等熱力學性質的研究和高分子在溶液中的遷移性質(包括高分子溶液的沉降、擴散和粘度)的研究都是高分子溶液基礎研究的重要方面。
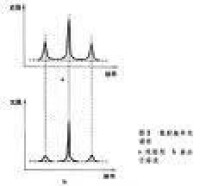
高分子溶液
高聚物的溶解比小分子化合物慢得多。溶解過程分為兩個階段:
由於非晶高聚物的分子鏈段的堆砌比較鬆散,分子間的作用力又弱,溶劑分子比較容易滲入非晶高聚物內部,使高聚物體積膨脹;而非極性的結晶高聚物的晶區分子鏈堆砌緊密,溶劑分子不易滲入,只有將溫度升高到結晶的熔點附近,才能使結晶轉變為非晶態,溶解過程得以進行。在室溫下,極性的結晶高聚物能溶解在極性溶劑中。
即以分子形式分散到溶劑中去形成均勻的高分子溶液。
交聯高聚物只能溶脹,不能溶解,溶脹度隨交聯度的增加而減小。

高分子溶液
高分子溶液(特別是那些溶劑的溶解能力較差的溶液)在降低溫度時往往會發生相分離,分成兩相,一相是濃相;另一相為稀相。濃相的粘度較大但仍能流動;稀相比分級前的濃度更低。往高分子溶液中滴加
沉澱劑也能產生相分離,高分子的相分離有分子量依賴性,因而可以用逐步沉澱法來對高聚物進行分子量的分級。
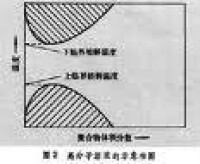
高分子溶液
在一定程度上仍可用極性相近原則來判定高分子的溶解度,即極性大的高聚物溶於極性大的溶劑,反之亦然。更精確一點的方法是通過比較高聚物和溶劑的溶度參數 δ,溶度參數δ 的定義是內聚能密度的平方根,它是物質凝聚態分子間相互作用能的一種量度。當高聚物和溶劑的溶度參數的差值Δδ 較大時(Δδ=|δp-δS|,δp為高聚物的溶度參數,δS為溶劑的溶度參數),高分子就不易溶於溶劑中;如果高聚物與溶劑的溶度參數極為接近,則高分子容易溶於溶劑中。粗略地從目前實驗得到的數據來看,對非極性溶劑來說,可以發生溶解的最大允許的Δδ 值約為±0.8,對
極性溶劑來說約為±3.4。由於分子間的相互作用和溶解過程比較複雜,因此用溶度參數來判定溶解性能仍有例外情況(見高聚物內聚能密度)。

高分子溶液
目前比較重要的高分子溶液理論有以下幾種:
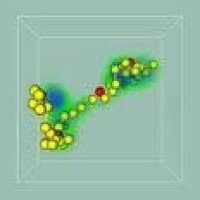
高分子溶液
弗洛里-哈金斯晶格理論 尺寸和形狀都相同的小分子混合物與理想溶液的偏離常歸因於混合熱的存在;但是溶液性質的非理想性也可由於分子尺寸有較大差別所造成。對高分子溶液而言,一個長鏈高分子的分子體積遠大於溶劑分子體積,而且鏈段間的鍵接使鏈段在晶格上的排布有一定的相關性。1942年P.J.弗洛里和M.L.哈金斯假定鏈段與溶劑分子具有相同的體積,都佔有一個晶格點(圖1),然後各自獨立地計算了n1個溶劑分子和n2個由x個鏈段連接而成的高分子在空間格子中的可區分的構象排布數目,導得構象混合熵ΔSm: ΔSm=-k(n1lnφ1+n2lnφ2) 式中φ1和φ2分別為溶劑和高分子的體積分數;k為玻耳茲曼常數。體系的混合熱ΔHm等於形成一個鏈段-溶劑接觸點所需的能量Δε乘以接觸點的數目: ΔHm=ZΔεn1φ2=kTχn1φ2
式中Z為晶格配位數;T為絕對溫度;χ=ZΔε/kT,稱作相互作用參數,又稱弗洛里-哈金斯參數。由此可得到混合自由能ΔGm: ΔGm=kT(n1lnφ1+n2lnφ2+χn1φ2)
並進一步導得各組分的偏摩爾混合自由能與各種溶液性質的理論關係。

高分子溶液
在弗洛里-哈金斯的晶格理論中,相互作用參數χ是高分子-溶劑體系中溶劑能力的量度,溶劑愈良,χ值愈小。χ值隨溫度的降低而單調上升,降低溫度會產生相分離,從而能說明上臨界溶解溫度的存在。晶格理論對臨界相分離條件和高分子在兩相中分配的分子量和濃度依賴性所作的分析與實驗事實基本相符,從而為高聚物的分級條件的選擇以及在分級數據的處理上提供了理論依據。

高分子溶液
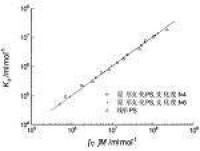
雖然弗洛里-哈金斯的晶格理論在高分子科學的發展上起了重要作用,但理論本身仍存在一些缺點,它無法說明在ΔHm=0的高分子溶液體系中χ值並不是零,也無法說明從滲透壓的第二維利係數(又譯維里係數)A2得到的χ值有分子量的依賴性,式中Μ1為溶劑的分子量;ρ1、ρ2為溶劑和高聚物的密度。從量熱學測定ΔHm時得到的χ值,有高分子濃度的依賴性。另一方面,高分子溶解時常伴隨有體積的改變,還發現升高溫度也能產生相分離,即存在一個下臨界溶解溫度(圖2)。對於這些事實,晶格理論也都沒有預計到。高分子溶液
高分子溶液
弗洛里-哈金斯理論的晶格模型忽略了一個實際問題,即在很稀的高分子溶液中,鏈段的空間分佈必然是非連續的,在高分子線團所在的區域鏈段的濃度很高,而在高分子線團之間卻為純溶劑所佔據。高分子的每一個鏈段都佔有一定的體積,在此體積中排除了其他鏈段進入的可能,通常稱為排除體積效應,它又依賴於溶劑的性質。在良溶劑中,高分子鏈段優先選擇溶劑分子作為近鄰,使高分子的實際尺寸和排除體積增大。相反地,在劣溶劑中排除體積卻減小。排除體積的理論計算是一個十分複雜的問題,但可以預期它應與相互作用參數χ有關。1950年弗洛里和W.R.克里格鮑姆假定高分子線團在溶液中近似球形,其中鏈段密度按高斯函數的形式分佈。他們計算了高分子稀溶液的熱力學函數,並提出了一個具有溫度量綱的參數θ(常稱為弗洛里溫度)。在T=θ時,高分子溶液的熱力學性質與理想溶液的偏差消失。θ點可以用改變溶液的溫度或改變溶劑的性質而達到。高分子在θ 溶劑中的尺寸相當於高分子鏈的鏈段間沒有相斥和相吸引力時的尺寸,常稱為無擾尺寸,此時,第二維利係數A2為零。

高分子溶液
弗洛里-哈金斯晶格理論保留了小分子正規溶液理論的主要特點,只是對相應的混合熵作了修正,以適應高分子的特殊性。它還假定混合時沒有體積變化,這些都與實際情況不符。
對應態原理說明,一對分子i和j之間的位能ε(rij)與它們之間的距離rij有關,它可以用一個普遍適用的位能函數Φ表示為:式中ε*和r*是反映分子結構的特徵參數,分別具有能量和長度的量綱。從這兩個特徵參數,又可以定義無量綱的對比溫度,對比體積和對比壓力這三個對比變數,將這些變數引入統計熱力學的配分函數,即可得到狀態方程,其具體形式只依賴於位能函數Φ的本質。在二元混合物中,各不同組分間的相互作用可用六個特徵參數描述。假設它們依從同一形式的位能函數 Φ,則可導得混合物的第二維利係數和混合時的體積變化。在原則上,從實驗數據可以計算相異組分間的相互作用,但在實際上直接計算ε*和r*還是困難的,需要藉助於各種簡化了的模型。狀態方程理論應用於混合物時,其最大的成功在於它能說明混合時體積的改變,這一改變在兩個組分的分子尺寸和相互作用差別較大時更為顯著,過量體積常為負值。狀態方程理論應用於高分子溶液時,可以正確地預計相互作用參數χ 的濃度依賴性並解釋下臨界溶解溫度的存在。標度理論 把鐵磁體在
居里點附近的相變理論應用於高分子鏈構象的處理。當鐵磁體冷到居里點溫度TC以下時,在沒有外磁場下,從整體說沒有磁矩,但在局部區域也有磁矩。與原子自旋取向相關的局部磁區的大小,即相關尺寸ξ的溫度依賴性為:式中τ為對比溫度;v為一個特徵冪數,此式在τ →0時成立。這個關係與一個孤立的柔性鏈高分子在良溶劑中的均方半隨
聚合度N 變化的情況相似。與鐵磁體相變理論的類比,可得出在d維晶格上的有排除體積效應的無規行走應符合v=3/(d+2)的結論。在三維時,v=3/5。標度理論只能得到兩個量之間的標度關係,即其中一個量增大一倍時另一個量應增大多少倍的問題,也即找出冪數關係的數值。標度理論也適合於處理柔性鏈高分子濃溶液。對於良溶劑,目前已經得出的重要結論是:濃溶液滲透,式中c 是濃度;線團的均方半徑隨濃度的變化應服從的規律。但這些結果還有待更多的實驗驗證。












