微分法
對函數局部變化率的線性描述
在數學中,微分是對函數的局部變化率的一種線性描述。微分可以近似地描述當函數自變數的取值作足夠小的改變時,函數的值是怎樣改變的。當某些函數f的自變數x有一個微小的改變h時,函數的變化可以分解為兩個部分。一個部分是線性部分,另一部分是比h更高階的無窮小,這種表示方法成為微分法。
微分法
微分法
在古典的微積分學中,微分被定義為變化量的線性部分,在現代的定義中,微分被定義為將自變數的改變數 映射到變化量的線性部分的線性映射。這個映射也被稱為切映射。給定的函數在一點的微分如果存在,就一定是唯一的。
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
在數學中,微分是對函數的局部變化率的一種線性描 述。微分可以近似地描述當函數自變數的取值作足夠小的改變時,函數的值是怎樣改變的。當某些函數 的自變數 有一個微小的改變 時,函數的變化可以分解為兩個部分。一個部分是線性部分:在一維情況下,它正比於自變數的變化量,可以表示成 和一個與 無關,只與函數 及 有關的量的乘積;在更廣泛的情況下,它是一個線性映射作用在 上的值。另一部分是比 更高階的無窮小,也就是說除以 后仍然會趨於零。當改變數 很小時,第二部分可以忽略不計,函數的變化量約等於第一部分,也就是函數在 處的 微分,記作 或。如果一個函數在某處具有以上的性質,就稱此函數在該點可微。
不是所有的函數的變化量都可以分為以上提到的兩個部分。若函數在某一點無法做到可微,便稱函數在該點不可微。
微分法定義如下:
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
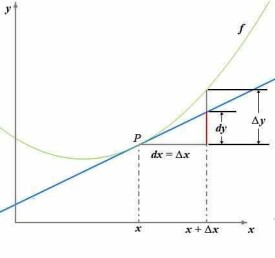
設函數 在某區間 內有定義。對於 那一點,當 變動到附近的(也在此區間內)時,如果函數的增量 可表示為(其中 是不依賴於 的常數),而 是比高階的無窮小,那麼稱函數 在點 是可微的,且 稱作函數在點 相應於自變數增量 的微分,記作,即,是 的線性主部。
微分法
微分法
微分法
微分法
通常把自變數 的增量 稱為自變數的微分,記作,即。
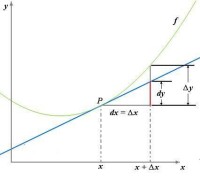
圖1.微分法
微分法
微分法
(函數在一點的微分,其中紅線部分是微分量,而加上灰線部分后是實際的改變數。)
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
微分法
設 是曲線 上的點 在橫坐標上的增量,是曲線在點 對應 在縱坐標上的增量,是曲線在點 的切線對應 在縱坐標上的增量。當 很小時,比 要小得多(高階無窮小),因此在點 附近,我們可以用切線段來近似代替曲線段。
微分法
微分法
和求導一樣,微分有類似的法則,例如,如果設函數、可微,那麼:
微分法
微分法
微分法
微分法
微分法
4)若函數 可是,那麼。
微分法
微分法
微分法
微分法
如果說微分是導數的一種推廣,那麼微分形式則是對於微分函數的再推廣。微分函數對每個點 給出一個近似描述函數性質的線性映射,而微分形式對區域 內地每一點給出一個從該點的切空間映射到值域的斜對稱形式: 。在坐標記法下,可以寫成:
微分法
微分法
微分法
微分法
微分法
微分法
微分法
其中的 是 -射影運算元,也就是說將一個向量 射到它的第 個分量 的映射。而 是滿足:
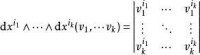
微分法
微分法
微分法
微分法
微分法
特別地,當 是一個從 映射到 的函數時,可以將 寫作:
微分法