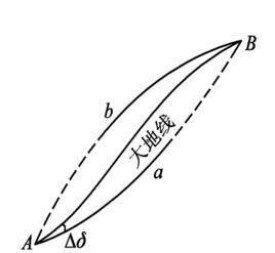
大地線(Geodesic Lines)是指地球橢球面上兩點間的最短程曲線。
在
微分幾何中,大地線(又稱測地線)另有這樣的定義:“大地線上每點的密切面(
無限接近的三個點構成的平面)都包含該點的曲面法線”,亦即“大地線上各點的主法線與該點的曲面法線重合”。因曲面法線互不相交,故大地線是一條空間曲面曲線。
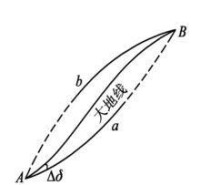
圖1-大地線示意圖
假如在橢球模型表面A, B兩點之間,畫出相對法截線如圖1,然後在A,B兩點上各插定一個
大頭針,並緊貼著
橢球面在大頭針中間拉緊一條細橡皮筋,並設
橡皮筋和橢球面之間沒有
摩擦力,則橡皮筋形成一條曲線,恰好位於相對法截線之間,如圖1所示,這就是一條大
地線,由於橡皮筋處於拉力之下,所以它實際上是兩點間最
短線。
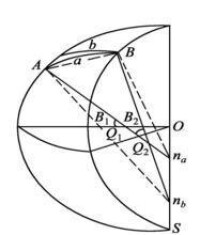
圖2-相對法截線示意圖
假設
經緯儀的縱軸同A,B 兩點的法線和重合(忽略垂線偏差),如此以兩點為測站,則經緯儀的照準面就是法截線。用A點照準B點,則照準面同橢球面的截線為AaB,叫A 點的正法截線,或B點的反法截線;同樣由B點照準 A 點,則照準面 與橢球面的截線為BbA,叫B點的正法截線,或A點的反法截線。因法線 和互不相交,故AaB和BbA 這兩條法截線不相重合。AaB 和BbA叫做A,B 兩點的相對法截線。註:與分別是 A ,B 兩點法線與短軸的交點。
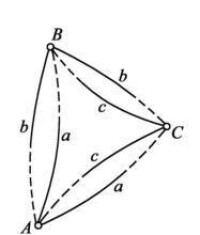
圖3
當A,B兩點位於同一子午圈或同一平行圈上時,正反法截線則合二為一,這是一種特殊情況。在通常情況下,正反法
截線是不重合的。因此在橢球面A,B,C三點處所測得的角度(各點上正法截線之夾角)將不能構成閉合三角形,見圖3。為了克服這個矛盾,在兩點間另選一條單一的大地線代替相對法截線,從而得到由大地線構成的單一的三角形。
1.大地線是橢球面上兩點間的最短線。
2.大地線是無數法截線的連線。
3.橢球面上的大地線是雙重彎曲的曲線。
4.大地線位於相對法截線之間。
5.不在同一子午圈與同一平行圈上的兩點的正反法截線是不重合的,他們之間的夾角為△,在一等三角測量中可達到千分之四。大地線是兩點間最短線,而且位於相對
法截線之間,並靠近正法截線(如圖1),它與正法截線的夾角
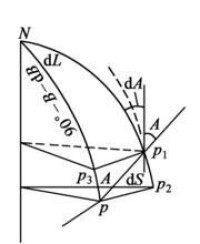
圖4
如圖4,設p 為大地線上任意一點,其經度L ,緯度為B,大地線方位角為A。當大地線增加dS 到p點時,則上述各量相應變化
dL ,
dB 及
dA。所謂大地線微分方程,即表達dL,dB,dA各與dS 的關係式。