群表示論
用具體矩陣群描述群的理論
群表示論用具體的線性群(矩陣群)來描述群的理論,是研究群的最有力的工具之一。在19世紀末和20世紀初它由F.G.弗羅貝尼烏斯和W.伯恩賽德獨立開創,而弗羅貝尼烏斯的工作則由I.舒爾所改善和簡化。
在群論中,群表示論(group representation theory)是一個非常重要的理論。它包含了(局部)緊緻群、李群、李代數及群概形的表示等種種分支,近來無限維表示理論也漸露頭角。表示理論在量子物理與數學的各領域中均有重要應用。
群表示論早期是藉矩陣的語言描述的,具體定義如次:
如果任何非零方陣的集合的乘法關係和給定群的乘法關係相同,則這個矩陣集合形成群的一個表示,這套矩陣的階稱為表示的維數。如果兩個同維表示的矩陣以同一相似變換相關聯,則稱這兩個表示是等價的。如果任何維數大於一的表示的所有矩陣都可以用相同的相似變換轉換為相同的塊對角矩陣結構,則稱此表示為可約表示,反之稱為不可約表示。形式地說,一個群G的表示乃一同態,其中V為給定的有限維向量空間,係數佈於一個域F,通常取R或C,但在一般域(如局部域或有限域)上的表示也有重要應用。GL(V)表從V上的自同構,或對一給定的基底來說,是階可逆方陣的集合。若Ker(ρ)是平凡的,則稱此表現是 忠實的。
若所考慮的群G帶有額外的結構(如拓撲群、李群或群概形),我們通常要求ρ滿足相應的條件(如連續性、可微性或者要求它是概形間的態射);在有限群及緊緻群以外的情況,通常也須考慮無窮維表示。
一個群G的所有有限維表示構成一個張量範疇,記為RepG;其態射定義如下:
它等價於有限維F[G]-模所構成的範疇。不難驗證表示間的同構確由矩陣的相似變換給出。一個表示被稱作不可約的,當且僅當它沒有在G的作用下不變的非平凡子空間。若一個表現能表成不可約表示的直和,則稱之為完全可約的。若取,則緊緻群的表示均為完全可約的,對於一般的李群及群概形則複雜得多,完全可約與否通常與半單性有關。
設G是有限群,V是複數域C上的有限維向量空間,GL(V)是V上全體可逆線性變換所組成的群。從G 映入GL(V)的一個同態(見公式1 )稱為G的一個表示,而V稱為ρ的表示空間。設U是V的 一個子空間,若(見公式2),則稱U是V(關於ρ)的一個不變子空間,這時ρ(g)在U上 的限制就給出G的一個表示(見公式3)如果沒有非零真不變子空間,就說V是不可約表示空間,而ρ稱為G的不可約表示;否則就說V和ρ是可約的。如果V有不可約不變子空間V1,V2,…,Vr使V是它們的直和即V=V1+V2+…+Vr,就說ρ 是完全可約的。這時,若ρi(g)=ρ(g)∣vi,則 記(見公式4),並說ρ分解成不可約表示ρ1,ρ2,…,ρr的和。有限群表示論的一個重要結果即馬施克定理:有限群的任一表示都是完全可約的。因此,研究有限群的表示只要研究它的不可約表示就夠了。
公式5
設ρ:G→GL(V)是有限群G的一個表示。如果選V的一個基υ1,υ2…,υn,並令(見公式5)
公式7
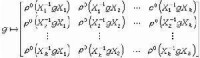
公式8
公式9
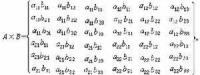
公式10
設H是有限群G的子群,x1,x2,…,xk是H在G中一左陪集代表系,ρ是H的一個表示。那麼,對每個g∈G規定ρG:(見公式8),式中(見公式9) ρG是G的一個表示,即所謂ρ的誘導表示。設ρ和ψ是G的兩個表示,規定,其中ρ(g)圱ψ(g)是矩陣ρ(g)和ψ(g)的克羅內克乘積,ρ圱ψ也是G的一個表示,即表示 ρ 與 ψ 的張量積。所謂 m×m 矩陣和n×n矩陣 的克羅內克乘積(張量積),是指。它是一個mn×mn矩陣。例如,當m=2,n=3時,(見公式10)設ρ:G→GL(V)是有限群G的一個表示。令χρ(g)=Trρ(g),,則Ⅹρ是定義在G上的函數。顯然它在G的共軛類上取相同的值,因此Ⅹρ是G的類函數,Ⅹρ稱為表示ρ的特徵標。當ρ不可約時,Ⅹρ稱為不可約特徵標。特徵標實際上確定了表示,可以證明,兩個表示等價,當且僅當它們的特徵標相等。利 用特徵標還可以證明,G只有有限個不同的不可約特徵標,其個數恰好等於G的共軛類的個數。因此研究有限群的不可約特徵標是有重要意義的。關於不可約特徵標有所謂正交關 系,即設Ⅹ1,Ⅹ2,…,Ⅹc是G的不同的不可約特徵標,g1,g2,…,gc是G的所有的不同的共軛類中的代表元,而h1,h2,…,hc是這些共軛類中元素個數,則有(見公式11、12) ,式中δij為克羅內克符號。
誘導表示的特徵標稱為誘導特徵標。表示的張量積的特徵標是相應特徵標的乘積。誘導特徵標及與其有關的弗羅貝尼烏斯互反律和特徵標乘積的分解,是表示論的主要工具。所謂弗羅貝尼烏斯互反律,即若ρ與ψ分別為G與H的不可約表示,則ψ在ρH(即ρ限制到H上)的完全分解中出現的重數等於ρ在誘導表示ψG的完全分解中出現的重數。對任意域F亦可象對複數域C那樣定義表示空間、表示及特徵標等。若F的特徵不整除有限群G的階,則仍然有表示的完全可約性,如果F 同時還是代數封閉的,那麼用F代替C,以上的討論成立。以n記有限群G的所有元素的階的最小公倍數。H.馬施克於1898年曾猜想G 的所有不可約表示皆可在n次分圓域Q(ξn)(ξn為n次本原單位根)中實現, 即如果Ⅹ是G的一個(在複數域C上的)不可約特徵標,那麼存在一個矩陣表示, 其特徵標即Ⅹ。R.(D.)布饒爾在1945年證明了這個猜想。
將群表示論應用於有限群的研究,最早的最著名的結果是伯恩賽德定理:階為pαqβ的群是可解群,這裡p、q是相異素數,α、β是非負整數。近年來這個定理雖已有了抽象群論的證明,但不如用表示論的原證簡捷。
20世紀20年代,E.諾特強調了“模”這一代數結構的重要性,她把有限群G的表示ρ:G→GL(V) 的表示空間V看成一個雙模,即除了域F的元素作為運算元(即V到V的自同態)外,還容許群環F【G】的元素g1,g2,…,gn是G的全部元素)作為運算元(見公式13):
並且適合條件(見公式14、15)的模。反之,給定一個有限維F【G】的模V,顯然每個g∈G在V上引起一個可逆線性變換,由此得到G的一個表示。對於F【G】的模,可以與上文完全平行地定義可約性、不可約性及完全可 約性。一個F【G】的模是可約的或不可約的或完全可約的,當且僅當G的相應的表示是可約的或不可約的或完全可約的。所謂一個代數A是半單的,是指所有的A模都是完全可約的。因此群代數F【G】是半單的。這樣,E.諾特就將代數結構論和群表示論融合為一,推進了這兩個分支的發展。
近50年來,布饒爾將群表示論的研究大為深化,他引進了模表示論,研究了群階除盡域的特徵的域上的表示,以及模表示與常表示(即C上的表示)的關係,而群表示論在有限群結構理論中起著日益重要的作用。在這方面的第一個重要結果是費特-湯姆森證明了有長期歷史的伯恩賽德猜想:奇數階群都是可解群。近年來則導致了有限單群分類問題的解決。(見有限單群)
有限群的表示論已推廣到無限群,特別是局部緊拓撲群,這成為近代分析的一個主要領域,推廣了經典的傅里葉分析。群表示論在理論物理和量子力學中有重要的應用。
給定G的一個表示,可以得到一個 特徵標,它是個類函數。特徵標理論在有限群分類中占關鍵地位;在緊緻群上,特徵標滿足舒爾正交關係,又根據 彼得-外爾定理,不可約表現的特徵標相對於 范數在類函數中稠密。請參見特徵標理論。
設H為G之子群,![(G:H)。以下將定義兩個函子(限制)與(誘導)。</div><div class=]() 若為G的表示,則ρ限制於H給出H的表示,記為。若為H的表示,我們定義。G以右乘法作用在V上。V仍是有限維,記此表示為。誘導表示亦可用矩陣直接計算,或定義為某個主齊性空間的截面;後者可推廣至李群與群概形的表示,此時誘導表示的性狀與G /H的幾何構造密切相關。
若為G的表示,則ρ限制於H給出H的表示,記為。若為H的表示,我們定義。G以右乘法作用在V上。V仍是有限維,記此表示為。誘導表示亦可用矩陣直接計算,或定義為某個主齊性空間的截面;後者可推廣至李群與群概形的表示,此時誘導表示的性狀與G /H的幾何構造密切相關。
弗羅貝尼烏斯互反定理言明:若V,W分別為G,H的表示,則有自然的同構。換言之:為一對伴隨函子。
若以特徵標表之,上述同構化為一個較弱但較具體的等式。
任意一個群G都自然地作用在其群代數上,稱為 正則表現。對稱群Sn以作用在上。以作用於m次調和多項式上。
