黎曼曲面

單值解析函數的反函數可以是多值的。例如，冪函數和指數函數的反函數為根式函數和對數函數，它們都是多值的。另外，從一個解析函數元素出發沿一個閉曲線作解析開拓，最後可能得到不同的元素。因此，完全解析函數往往是多值的。在研究多值函數時，人們先把它分解為一個個單值解析分支，然後按這些分支之間的關係把它們連接起來。

為研究，把擴充的複平面沿正實軸割開，記為╦1,它的邊界是兩條正實軸Л劑和Л奐，分別鑲在第一象限的下邊和第四象限的上邊，在╦1上令

就得到的一個單值解析分支，它在╦1的內部是解析的，並且連續到邊界Л劑和Л奐上, 但在和同一個正實數x對應的分別位於Л劑 和Л奐上的兩個點上,卻分別取不同的值。設╦ 2是另一個沿正實軸割開的擴充的複平面，它的邊界記為Л崹 和Л崍。令

就得到的另一個單值解析分支。與不同，在Л崹和Л崍 上與正實數x對應的兩個點處，的值分別是。由於在 Л劑和Л奐上的值分別與在Л崍和Л崹上的值相同，人們自然地把Л劑 和Л崍以及Л奐和Л崹兩兩粘接起來，而把╦1和╦2拼接成一個整體，這就是的黎曼曲面。作為定義在這個曲面上的函數，包含了它的兩個分支，同時是單值的。替多值函數構造一個適當的定義場所，而使得它成為一個完整的單值解析函數，這是黎曼的原始的思想。這樣構造出來的,和lnz的黎曼曲面如圖1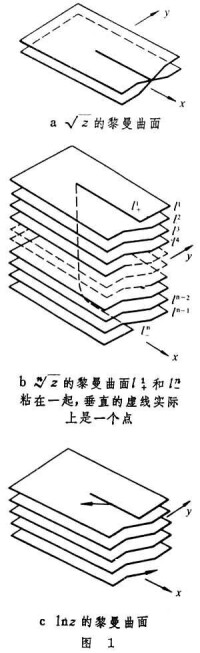所示。

把 的黎曼曲面按原來的位置放在擴充的複平面上就成了擴充複平面的一個n 葉覆蓋曲面。曲面上的點O和∞叫做n-1級枝點。同樣,lnz的黎曼曲面是（除去原點后的）複平面的無枝點的覆蓋曲面。一般地說，複平面（或擴充的複平面）的任意的一個覆蓋曲面都可看作一個黎曼曲面。設覆蓋曲面中的點P位於複平面中的點z之上，則稱z為P的投影。定義在曲面上的一個函數在非枝點處是否解析，就看它作為投影z的函數是否是解析的；而在投影為z0的n-1級枝點處，則要看它對於是否是解析的。這就是黎曼本人的原始的黎曼曲面的概念。黎曼曲面的經典理論是在這樣的概念上發展起來的。

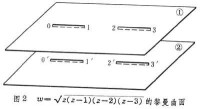
一個完全解析函數或完全解析構形，把其中以z0為中心的函數元素看作放在z0上的點，自然就成了擴充平面的覆蓋曲面，這就是它的黎曼曲面。一個代數函數w=w(z)的黎曼曲面是擴充平面的n葉覆蓋曲面（n為對應的方程中w 的最高次數）。例如，

的黎曼曲面的構造如圖2所示。把上下兩個平面中連接0,1和連接2,3的兩個線段都割成裂縫，每一裂縫產生兩條邊，分別與平面上半部分和下半部分相連，用實線與虛線表示。然後把上平面中實線（虛線）所示的邊和下平面中虛線（實線）所示的邊粘接起來。

（C.H.）H.外爾首先給出黎曼曲面的近代定義。與此同時，他也給出了"流形"這個近代數學的基本概念的嚴格定義。按照外爾的觀點，黎曼曲面就是一維的複流形。在一個曲面(局部與歐氏平面同胚的、連通的豪斯多夫空間) 上，定義了一族局部參數（曲面的某一個開集上的一個連續單葉復值函數，也叫局部坐標），若在任意兩個相鄰的局部參數的定義域的公共部分上，其中的一個參數作為另一個參數的函數是解析的，並且這些參數的定義域覆蓋了整個曲面，那麼，這個曲面連同這族局部參數（叫做共形結構）就構成了一個黎曼曲面。複平面C或者C上任一個區域按其自然參數都是黎曼曲面。在擴充複平面╦上，除了在C上已有一個自然參數外，再在區域{z││z│>0}（包括無窮遠點）上令,得另一參數，而使╦成為一個黎曼曲面。一個黎曼曲面到黎曼曲面里的連續映射稱為是解析的，如果它用兩個曲面上的局部參數表示出來是解析函數。一個黎曼曲面到 ╦里的解析映射就是該曲面上的半純函數（亞純函數）。黎曼曲面上的調和（或次調和）函數的定義為關於局部參數是調和（或次調和）的函數。黎曼曲面的引入大大地開擴了複變函數論的研究範圍。

由緊曲面作成的黎曼曲面叫做閉黎曼曲面，否則就叫做開黎曼曲面。若一個閉曲面（或開曲面）上的一維同調群（或模理想邊界的一維同調群）的秩是2g，則稱g (非負整數或無窮)為此黎曼曲面的虧格。開曲面的虧格可能為無窮。兩個黎曼曲面稱為是共形等價的，如果存在一個從一個曲面到另一個曲面上的一一的解析映射（共形映射）。同一個虧格g(g>1)的閉黎曼曲面的所有共形等價類組成所謂模空間。黎曼首先發現，模空間中的元素由3g-3個復參數確定。從模空間的研究中產生出豐富多採的泰希米勒空間的理論。

人們還把開黎曼曲面作了分類。不存在非常數的負次調和函數的開曲面叫做拋物型曲面，其他的開曲面就叫做雙曲型曲面。拋物型曲面所成的類用OG表示。不存在非常數的有界解析或調和函數，狄利克雷積分為有窮的解析或調和函數，或正調和函數的開曲面分別組成類OAB或OHB，OAD或OHD,或OHP。在這些曲面類之間存在如下的包含關係：

按照黎曼本人的原始概念，黎曼曲面是╦ 的覆蓋曲面。所謂曲面愞 是曲面F的覆蓋曲面，是指存在曲面愞到曲面F里的映射ƒ,對於每一個慉 ∈愞，都存在慉和ƒ(慉)∈F的開鄰域 和V，使得限制在和V之間，ƒ拓撲等價於單位圓到自身的映射z→=zn（n是正整數，它與慉有關；當n>1時，慉叫做枝點）。定義中的映射ƒ叫做投影。當F是一個黎曼曲面時，可使上面的是F 的局部參數。令z為愞的局部參數，就在愞上定義了一個共形結構，而使它成為一個黎曼曲面，並且，ƒ是一個解析映射。一個完全解析函數w =g(z)的黎曼曲面就是╦的覆蓋曲面，並按上面的方法賦以共形結構。在這個曲面上有兩個半純函數：把w=g(z)看作曲面上的單值函數，記以w=G(P)；還有從曲面到╦上的投影，記以z=Z(P)，P是曲面上的點。這裡的完全解析函數可以包含極元素和分枝元素，以及分枝的極元素。

在一個曲面上有相同的起點和相同的終點的兩條曲線（連續曲線）уi:t→φi(t)(0≤t≤1,i=1,2) 稱為是同倫的，如果存在到這個曲面里的連續映射(t,u)→φ(t，u)(0≤t≤1,0≤u≤1)，使得φ(t,0)呏φ1(t),φ(t,1)呏φ2(t),φ(0,u)呏φ1(0),φ(1,u)呏φ1(1)。曲面上固定端點的閉曲線組成的所有同倫等價類以曲線的連接作為乘法運算組成一個群，叫做曲面關於這個定點的基本群。關於不同點的基本群是互相同構的。基本群只包含一個元素的曲面叫做單連通曲面。

沒有枝點的覆蓋曲面叫做光滑覆蓋曲面。設ƒ使愞成為F 的光滑覆蓋曲面。若у=ƒ()，其中的和у分別是愞和F上的曲線，則稱是у的提升。若對於任意的у嶅F和任意的以у的起點為投影的慉∈愞，у的以慉為起點的提升總是存在的，則稱愞是F的正規覆蓋曲面。光滑性保證指定起點的提升的惟一性。單值性定理稱：若愞是F的正規覆蓋曲面，則對於F上的任意兩條互相同倫的曲線v1和v2以及愞中任意的以v1和v2的公共起點為投影的點慉,v1和у2的以慉為起點的提升和2總有公共的終點，並且,1和2也是同倫的（在 愞上）。複變函數論中關於解析函數元素沿曲線解析開拓的單值性定理是這個定理的一個具體應用。

單連通的正規覆蓋曲面叫做萬有覆蓋曲面。對於任意的一個曲面F，它的萬有覆蓋曲面愞總是存在而且在共形等價的意義下是惟一的。當F是一個黎曼曲面時，可使愞也成為一個黎曼曲面，而投影ƒ是解析映射。著名的單值化定理稱：單連通的黎曼曲面一定共形等價於 ╦(閉)、C（拋物型）或單位圓（雙曲型）。若愞=╦，則F=╦。如果愞 =C，則F =C,C \{0}, 或是環面（環面就是虧格為1的閉曲面；反過來, 環面的萬有覆蓋（黎曼）曲面一定是C）。當愞是單位圓時，所有滿足ƒ。φ=ƒ 的共形映射φ（叫做覆蓋變換）組成一個富克斯群。因此，除去上面幾種特例外，每一個黎曼曲面都可表示成單位圓關於一個富克斯群的商；因而,分式線性變換組成的間斷群(即克萊因群，包括富克斯群)的理論和黎曼曲面理論有緊密的聯繫。若這裡的F是完全解析函數w=g(z)的黎曼曲面，則G(ƒ(t))和Z(ƒ(t))（t∈╦，C，或單位圓）都是半純函數，多值函數w=g(z)經參數t（叫做單值化參數）單值化了。從而就解決了著名的希爾伯特第22問題即單值化問題。

在一個黎曼曲面上，若對每一個局部參數z都定義了一個微分ƒ(z)dz（ƒ(z)是半純函數）, 而與相鄰的兩個參數z和ζ 對應的ƒ(z)dz和φ(ζ)dζ 滿足關係ƒ(z(ζ))·z┡(ζ)=φ(ζ),則稱在曲面上定義了一個半純微分。半純函數(或半純微分)在某一點的零點或極點的級等於在取定一個局部參數后該函數（或該微分在這個參數下的表示形式中的係數）作為這個局部參數的函數在該點的零點和極點的級。黎曼－羅赫定理稱：在一個虧格為g的閉曲面上，指定了點p1,p2,…,ps;q1,q2,…,qt和正整數k1,k2,…,ks;n1,n2,…,nt,令。設以pi為至多ki級極點(或至少ki級零點，i=1,2,…,s)，並且以qi為至少ni級零點（或至多ni級極點，i=1，2,…，t）的所有半純函數(或半純微分)組成的複數域上的線性空間的維數為A（或B），那麼，A=B +m-g+1。這個定理是閉黎曼曲面理論的一個基本結果；在一定條件下，也被推廣到開曲面和高維複流形。

參考書目

H.Weyl.Die ldee der RieMannschen Fiche,Teubn-er,Leipzig,1913.

G.Springer,lntroduction to RieMann Surfaces,Addison-Wesley, Reading, Mass.,1957.

L. V. Ahlfors and L. Sario,RieMann Surfaces,Princeton Univ.　Press,　Princeton,　1960.