阻尼振動
振動系統受到摩擦阻力衰減的振動
阻尼振動:由於振動系統受到摩擦和介質阻力或其他能耗而使振幅隨時間逐漸衰減的振動,又稱減幅振動、衰減振動。不論是彈簧振子還是單擺由於外界的摩擦和介質阻力總是存在,在振動過程中要不斷克服外界阻力做功,消耗能量,振幅就會逐漸減小,經過一段時間,振動就會完全停下來。這種振幅隨時間減小的振動稱為阻尼振動.因為振幅與振動的能量有關,阻尼振動也就是能量不斷減少的振動.
機械振動按振幅的變化可分為阻尼振動(減幅振動)和無阻尼振動(等幅振動).
另外一種是受迫等幅振動.物體在振動的過程中有能量的輸出(損耗),系統又從外界輸入了能量,正好補償了在振動過程中所輸出(損耗)的能量.這種振動系統的能量和振幅都保持不變.這種無阻尼運動並不是不受阻力。
能量減少的方式有兩種:
一種是由於摩擦阻力的作用使振動系統的能量逐漸轉化為熱運動的能量.例如單擺擺動的過程中振幅減小或停下來就是由於系統的阻力作用使擺的機械能轉化為空氣的內能.
另一種是振動系統引起周圍物質的振動,使能量以波的形式向四周發出.例如:琴弦發出聲音不僅因為有空氣的阻力要消耗能量,同時也因為以波的形式輻射而減少能量.最後琴弦會停止振動.
當阻尼很小時,在一段不太長的時間看不出振幅有明顯的減小,就可以把它當作簡諧運動來處理.
如圖,以液體中的彈簧振子為例,介紹阻尼振動的動力學方程。
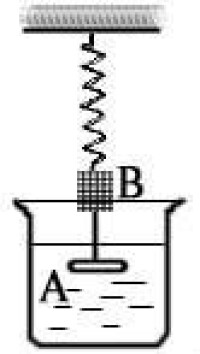
阻尼振動
對物塊應用牛頓第二定律:
為二階線性常係數齊次方程,即阻尼振動的動力學方程。
上述⑴式方程的特徵根:
阻尼振動的微分方程有三種不同形式的解,具體如下。
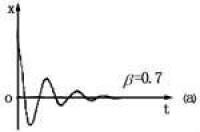
阻尼振動
即:,則:
解為:
說明振動變慢(由於阻力作用)
振幅為隨時間的推移,呈指數遞減,越大,振動衰減越快;越小,振幅衰減越慢。
定義:
表示阻尼大小的標誌,稱對數減縮,即經過一個周期后,振幅的衰減係數。
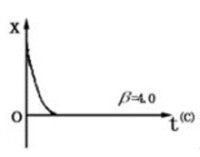
阻尼振動
即:,則方程的解為:
⑶
其中:由初始條件決定。
隨時間的推移,質點坐標單調地趨於零。質點運動是非周期的,甚至不是往複的。將質點移開平衡位置后釋放,質點便慢慢回到平衡位置停下來,即過阻尼狀態。
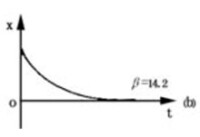
阻尼振動
即:,則方程的解為:
其中:由初始條件決定。
此種狀態,質點仍不往複運動。由於阻力較前者小,質點移開平衡位置釋放后,質點很快回到平衡位置並停下來。如圖示。
例如:天平的指針最好處於臨界阻尼狀態。(理想)
電流表、電壓表的指針最好處於臨界阻尼狀態,有時處於欠阻尼狀態。