共找到6條詞條名為焦點的結果 展開
焦點
數學術語
在幾何,焦點(focus或foci)是指構建曲線的特殊點。例如,一個或兩個焦點可用於定義圓錐截面,其四種類型是圓形,橢圓形,拋物線和雙曲線。此外,使用兩個焦點來定義卡西尼橢圓和笛卡爾橢圓,並且使用兩個以上焦點來定義橢圓。
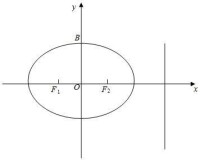
焦點
橢圓可以定義為到兩個給定焦點的距離之和為常數的點的軌跡。
圓是橢圓的特殊情況,其中兩個焦點彼此重合。因此,可以更簡單地將圓定義為每個距離單個給定焦點的固定距離的點的軌跡。也可以將圓定義為阿波羅尼奧斯圓,就兩個不同的焦點而言,作為具有與兩個焦點的距離的固定比例的點集合。
拋物線是橢圓的極限情況,其中的一個焦點是無限遠的點。
雙曲線可以定義為到兩個給定焦點的距離之間的差的絕對值為常數的點的軌跡。
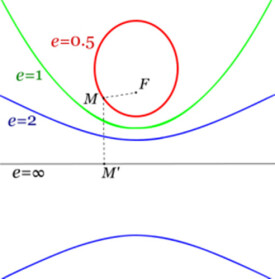
根據焦點和方向定義圓錐
還可以根據焦點和直線來描述所有的圓錐截面,這是一條不包含焦點的給定線。圓錐被定義為到每個焦點的距離相除點的軌跡是固定的正數,稱為偏心率e。如果e在0和1之間,則圓錐是橢圓;如果e = 1,圓錐是拋物線; 如果e> 1,圓錐曲線是雙曲線。如果到焦點的距離是固定的,並且直線是無限遠的線,那麼偏心率為零,那麼圓錐是圓。
根據焦點和直線圓定義圓錐
也可以將所有的圓錐截面描述為與單個焦點和單個圓形方陣等距的點的軌跡。對於橢圓,圓心的焦點和中心都有有限坐標,並且圓心的半徑大於圓的中心與焦點之間的距離;因此,焦點在內線圈內。這樣生成的橢圓的第二個焦點位於圓心的中心,橢圓完全在圓內。
對於拋物線,陣列的中心移動到無窮遠點(參見投影幾何)。直線“圓”變為零曲率的曲線,與直線不可區分。拋物線的兩臂隨著它們的延伸而變得越來越平行,“無窮遠”變得平行;使用投影幾何原理,兩個平行線在無窮遠點相交,拋物線成為閉合曲線(橢圓投影)。
為了產生雙曲線,選擇直線圓的半徑小於該圓的中心與焦點之間的距離;因此,焦點是在直線圓圈之外。雙曲線接近漸近線的雙臂和雙曲線的一個分支的“右手”臂與無限遠點處的雙曲線另一分支的“左手”臂相遇;這是基於這樣的原則:在投影幾何中,單線在無限遠的地方遇到自己。因此,雙曲線的兩個分支是無限遠的曲線的兩個(扭曲的)一半。
在投影幾何中,所有圓錐曲線是相同的,因為每個定義都可以為其他定義。
天文意義
在引力雙體問題中,兩個體彼此的軌道由兩個重疊的圓錐截面描述,其中一個物體的焦點與另一個物體的焦點之一在兩個物體的重心處重合。
因此,例如,冥王星的最小月亮有一個橢圓軌道,在冥王星系統的重心中有一個點,這是一個兩點之間的空間點。並且冥王星也以橢圓中的一個焦點移動到身體之間的同一個重心。冥王星的橢圓完全在Charon的橢圓內。
相比之下,地球的月球與其中一個焦點位於月球和地球重心的橢圓中,這個重心位於地球本身之內,而地球(更準確地說,它的中心)以一個焦點移動到一個橢圓中在地球內同樣的重心。重心距離地球中心至地面的四分之三。
此外,冥王星系統與太陽一起圍繞其重心移動一個橢圓形,地球 - 月球系統(以及太陽系中的每個其他行星月球系統或無月球星球)也是如此。在這兩種情況下,重心都在太陽體內。
笛卡爾橢圓是每個點的集合,與兩個給定焦點的距離的加權和是一個常數。如果權重相等,則會出現橢圓的特殊情況。
卡西尼橢圓是每個點的集合,其中兩個給定焦點的距離的乘積是常數。
一個n-橢圓是與n個焦點具有相同的距離總和的點集合。(n = 2的情況是傳統的橢圓)
焦點的概念可以推廣到任意代數曲線。令C為類m的曲線,令I和J表示無限遠的圓點。通過I和J中的每一個繪製m切線到C中。有兩組m行將具有m2點交點,在某些情況下由於奇異點而異。這些交點是定義為焦點,換句話說,如果PI和PJ都與C相切,則點P是焦點。當C是實曲線時,只有共軛對的交點是真實的,因此在實際焦點和m2-m假想焦點。當C是二次曲線時,以這種方式定義的真實焦點恰好是可以用於C的幾何構造的焦點。
令P1,P2,...,Pm作為類m的曲線C的焦點。令P是這些點的切線方程的乘積,Q是無窮大圓形點的切線方程的乘積。那麼P = 0和Q = 0的共同切線的所有線都與C相切。因此,通過AF + BG定理,C的切線方程式具有HP + KQ = 0的形式。由於C具有等級m,所以H必須是常數K而是小於或等於m-2。 H = 0的情況可以作為退化消除,因此C的切線方程可以寫為P + fQ = 0,其中f是任意多項式m-2。
例如,令P1 =(1,0),P2 =( - 1,0)。切線方程為X + 1 = 0,X-1 = 0,因此P = X2-1 = 0。無限循環點的切線方程為X + iY = 0,X-iY = 0,因此Q = X2 + Y2。因此,給定焦點的二次曲線的切線方程為X2-1 + c(X2 + Y2)= 0或(1 + c)X2 + cY2 = 1,其中c為任意常數。