模糊綜合評判

比如，要判定某項產品設計是否有價值，每個人都可從不同角度考慮：有人看是否易於投產，有人看是否有市場潛力，有人看是否有技術創新，這時就要根據這多個因素對事物作綜合評價。具體過程是：將評價目標看成是由多種因素組成的模糊集合（稱為因素集u），再設定這些因素所能選取的評審等級，組成評語的模糊集合（稱為評判集v），分別求出各單一因素對各個評審等級的歸屬程度（稱為模糊矩陣），然後根據各個因素在評價目標中的權重分配，通過計算（稱為模糊矩陣合成），求出評價的定量解值。上述過程即為模糊綜合評判。

20世紀80年代初，汪培庄提出了綜合評判模型，此模型以它簡單實用的特點迅速波及到國民經濟和工農業生產的方方面面，廣大實際工作者運用此模型取得了一個又一個的成果。與此同時，還吸引了一些理論工作者對此模型進行深化和擴展研究，出現了一批誘人的成果，諸如：多級模型、運算元調整、範疇統觀等等。

而且，針對實際應用中模糊綜合評判模型常遇到的一些問題，對其進行了改進，可採用多層次模糊綜合評判模型和廣義合成運算的模糊綜合評判模型。

綜合考慮事物多種因素，用模糊集理論來評定其優劣的方法。模糊綜合評判廣泛用於評定產品質量、環境質量、農業布局、天氣預報、醫療診斷等方面。

設給定兩個有限論域：U={u1，u2，…，un}，V={v1，v2，…， vm}。這裡U是綜合評判的因素所組成的集合,V代表評語所組成的集合。模糊綜合評判是一個模糊變換問題：X⋅R=Y

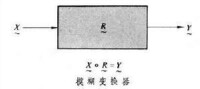
式中“⋅ ”表示合成運算，X是U上的模糊子集，評判結果Y是V上的模糊子集，模糊關係R可看作一個模糊變換器（見圖）。若已知Y和R，求X；或已知X和Y，求R；就構成模糊綜合評判的逆問題，需要求解模糊關係方程。模糊關係方程是法國學者E.桑傑斯於1976年根據醫療診斷的需要提出來的。這類問題相當於已知評判結果和模糊關係，求評判者對各種因素的權數分配問題。這種問題具有重大的實際意義，對發展專家系統起指導作用。

現舉評判電視機的實例來說明模糊綜合評判的方法。U={u1，u2，u3}，V={v1，v2，v3，v4}。這裡u1代表圖像,u2代表音響，u3代表價格；v1表示很好，v2表示較好,v3表示可以,v4表示不好。設聘請專家或顧客進行評判。例如對於圖像，有50%的人認為很好，40%的人認為較好，10%的人認為可以，沒有人認為不好。全部結果記作：

對於圖像：Vu1=(0.5，0.4，0.1，0)

對於音響：Vu2=(0.4，0.3，0.2，0.1)

對於價格：Vu3=(0，0.1，0.3，0.6)

這樣就構成一個模糊矩陣：設一類顧客在購買電視機時主要是要求圖像清晰，價格便宜，音響稍差則不要緊，則此類顧客對電視機三個因素的權數分配X =【0.5　0.2　0.3】

對電視機的評判結果為 這是根據最大最小運算得到的，還需作歸一化處理。因為0.5+0.4+0.3+0.3=1.5，用1.5除各項得到【0.330.27 0.20 0.20】。模糊綜合評判的結果，認為圖像、音響、價格都很好的佔比重最大，達33%。