晶體學點群
晶體學點群
在晶體學中,晶體學點群是對稱操作(例如旋轉、反映)的集合。這些操作以固定的中心向其他方向移動能使晶體復原,因此稱為對稱操作。對於一種真正的晶體(不是准晶體),點群對應的操作必須能夠保持晶體的三維平移對稱性。經過它的點群中任何操作之後,晶體的宏觀性質依然和操作前完全相同。在晶體的分類中,每一種點群也稱為晶類。
這樣看來似乎有無窮多種三維點群。然而,根據晶體局限定理可知,無窮多族的普通點群可以概括成32種晶體學點群。這32種點群與1830年約翰·弗里德里希·克里斯蒂安·赫塞爾提出的32種晶體形態學(外部)對稱性是等價的,而他是從觀察晶體外形得出的此結論。

晶體學點群
晶體學點群
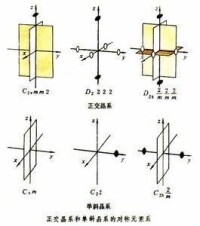
與晶體的32種對稱元素系相對應的對稱動作群。各種晶體的(理想)多面體外形會呈現出不同類型的對稱性。這些晶體的對稱性可用對稱元素n重旋轉和n重反組合成的各種對稱元素系反映對應的最基本的對稱動作是繞軸旋轉360°/n對應的最基本對稱動作是繞軸旋轉360°/n緊接以一個倒反動作,倒反動作據以進行的點應在軸線上)。基於晶體內部是具有點陣式的三維周期性結構,可以證明,晶體中允許存在的對稱軸的軸次n僅限於1、2、3、4、6,即晶體外形中可能呈現的對稱元素只限旋轉軸 和反軸,此中一重反軸即對稱中心,二重反軸即鏡面。晶體外形可能歸屬的對稱類型共有32種,對應於32種對稱元素系。

晶體學點群
晶體學點群
由於32種對稱元素系都至少有一個相交的公共點並各與一套能使晶體(理想)外形復原的點對稱動作群(實行對稱操作時,對稱物體至少有一點是不動的動作,稱為點對稱動作)相對應,這32種對稱元素系對應的對稱動作群稱做晶體學點群。
晶體在宏觀觀察中,在平行方向上呈現為具有均勻性的物體。由於結構中任何對稱動作所包含的平移已被均勻性所掩蓋,晶體結構中含平移的螺旋軸和滑移面在晶體宏觀性質中將表現為相應的旋轉軸和鏡面。晶體宏觀性質和晶體外形的對稱類型均以晶體微觀對稱性為基礎,也即晶體學點群以晶體學空間群為基礎。
熊夫利記號中大寫字母T、O、C、D、S代表四面體群、八面體群、雙面群、反軸群等,小寫字母i、s、v、h和d代表對稱中心、鏡面、通過主軸鏡面、與主軸垂直鏡面、等分兩個副軸的鏡面。單斜晶系一般取b為主軸,其他晶系一般取c為主軸。晶體學點群

晶體學點群
晶體學點群
晶體在衍射效應中,若將比率極小的反常散射忽略不計,則衍射強度在三維空間中將呈現具有對稱中心的對稱性。這一實驗現象稱為夫里德耳定律。基於這一定律,晶體衍射強度分佈的對稱類型只能屬於32個對稱元素系中11個含對稱中心者,與之對應的11個點群(即)稱為勞厄點群。
點群表示的是晶體所包含的對稱元素。目前有多種不同的記號,分別由結晶學家、礦物學家、物理學家和化學家使用。
對於下面兩種不同系統的關係,請參見 晶系。
熊夫利記號
主條目:熊夫利記號
• 更多資料:三維點群
在熊夫利中,點群是用字母符號加上數字下標表示的。下面簡述晶體學中使用的這種符號的意義:
• Cn(循環群)表示該群有一根n次旋轉軸。Cnh是Cn加上一個與旋轉軸垂直的鏡面(反映)對稱元素。Cnv則是Cn加上n個與旋轉軸平行的鏡面對稱元素。
• S2n(源自德語Spiegel,意思是鏡面)表示一根只含有2n次旋轉反映軸(簡稱映軸)。
• Dn(二面體群)表示這個群只有一根n次旋轉軸和n根垂直於這根主軸的二重軸。Dnh是加上一個與n次旋轉軸垂直的鏡面。Dnd則是Dn是加上n個與n次旋轉軸平行的鏡面。
• 字母T(四面體)表示這個群有四面體的對稱性。Td則包括了旋轉反映操作,T群本身則不包含旋轉反映操作,Th則是T群加上與旋轉軸垂直的鏡面。
• 字母O(八面體)表示該群具有八面體或者立方體的對稱性,可能包括(Oh)或不包括(O)旋轉反映操作。
根據晶體局限定理,在二維或三維空間中n的取值只有1、2、3、4和6。
| n | 1 | 2 | 3 | 4 | 6 |
| Cn | C1 | C2 | C3 | C4 | C6 |
| Cnv | C2v | C3v | C4v | C6v | |
| Cnh | C1h | C2h | C3h | C4h | C6h |
| Dn | D2 | D3 | D4 | D6 | |
| Dnh | D2h | D3h | D4h | D6h | |
| Dnd | D2d | D3d | D4d | D6d | |
| S2n | S2 | S4 | S6 | S8 | S12 |
D4d和D6d實際上是不存在的,因為它們分別包含了和12的旋轉反映軸。表格中剩下的27種點群與T、Td、Th、O和Oh共同組成32種晶體學點群。
赫爾曼–莫甘記號
主條目:赫爾曼–莫甘記號
赫爾曼–莫甘記號的一種簡略形式廣泛用於表示空間群,也用於描述晶體學點群。群的名稱列在下表中:
| 1 | 1 | |||||
| 2 | ⁄m | 222 | m | mm2 | mmm | |
| 3 | 3 | 32 | 3m | 3m | ||
| 4 | 4 | ⁄m | 422 | 4mm | 42m | ⁄mmm |
| 6 | 6 | ⁄m | 622 | 6mm | 62m | ⁄mmm |
| 23 | m3 | 432 | 43m | m3m |
| 晶族 | 晶系 | 赫爾曼–莫甘(完整記號) | 赫爾曼–莫甘(簡寫記號) | 舒勃尼科夫 | 熊夫利 | 軌形記號 | 考克斯特記號 | 順序 |
| 三斜 | 1 | 1 | C1 | 11 | [ ] | 1 | ||
| x | [1,2] | 2 | ||||||
| 單斜 | 2 | 2 | C2 | 22 | [2] | 2 | ||
| m | m | * | [ ] | 2 | ||||
| 2/m | C2h | 2* | [2,2] | 4 | ||||
| 正交 | 222 | 222 | 222 | [2,2] | 4 | |||
| mm2 | mm2 | C2v | *22 | [2] | 4 | |||
| mmm | D2h | *222 | [2,2] | 8 | ||||
| 四方 | 4 | 4 | C4 | 44 | [4] | 4 | ||
| S4 | 2x | [2,4] | 4 | |||||
| 4/m | C4h | 4* | [2,4] | 8 | ||||
| 422 | 422 | D4 | 422 | [4,2] | 8 | |||
| 4mm | 4mm | C4v | *44 | [4] | 8 | |||
| 2m | 2m | D2d | 2*2 | [2,4] | 8 | |||
| 4/mmm | D4h | *422 | [4,2] | 16 | ||||
| 六方 | 三方 | 3 | 3 | C3 | 33 | [3] | 3 | |
| 3x | [2,6] | 6 | ||||||
| 32 | 32 | D3 | 322 | [3,2] | 6 | |||
| 3m | 3m | C3v | *33 | [3] | 6 | |||
| 2/m | 2/m | D3d | 2*3 | [2,6] | 12 | |||
| 六方 | 6 | 6 | C6 | 66 | [6] | 6 | ||
| C3h | 3* | [2,3] | 6 | |||||
| 6/m | C6h | 6* | [2,6] | 12 | ||||
| 622 | 622 | D6 | 622 | [6,2] | 12 | |||
| 6mm | 6mm | C6v | *66 | [6] | 12 | |||
| m2 | m2 | D3h | *322 | [3,2] | 12 | |||
| 6/mmm | D6h | *622 | [6,2] | 24 | ||||
| 立方 | 23 | 23 | T | 332 | [3,3] | 12 | ||
| 3 | m3 | Th | 3*2 | [3,4] | 24 | |||
| 432 | 432 | O | 432 | [4,3] | 24 | |||
| 3m | 3m | Td | *332 | [3,3] | 24 | |||
| 3 | m3m | Oh | *432 | [4,3] | 48 | |||
