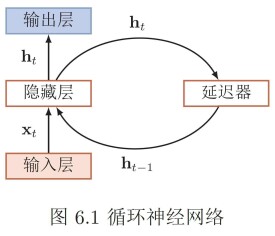
循環神經網路
遞歸神經網路
循環神經網路(RecurrentNeuralNetwork,RNN)是一類以序列(sequence)數據為輸入,在序列的演進方向進行遞歸(recursion)且所有節點(循環單元)按鏈式連接的遞歸神經網路(recursiveneuralnetwork)。
對循環神經網路的研究始於二十世紀80-90年代,並在二十一世紀初發展為重要的深度學習(deeplearning)演演算法,其中雙向循環神經網路(BidirectionalRNN,Bi-RNN)和長短期記憶網路(LongShort-TermMemorynetworks,LSTM)是常見的的循環神經網路。
循環神經網路具有記憶性、參數共享並且圖靈完備(Turingcompleteness),因此能以很高的效率對序列的非線性特徵進行學習。循環神經網路在自然語言處理(NaturalLanguageProcessing,NLP),例如語音識別、語言建模、機器翻譯等領域有重要應用,也被用於各類時間序列預報或與卷積神經網路(ConvoutionalNeuralNetwork,CNN)相結合處理計算機視覺問題。
1933年,西班牙神經生物學家Rafael Lorente de Nó發現大腦皮層(cerebral cortex)的解剖結構允許刺激在神經迴路中循環傳遞,並由此提出反響迴路假設(reverberating circuit hypothesis)。該假說在同時期的一系列研究中得到認可,被認為是生物擁有短期記憶的重要原因。隨後神經生物學的進一步研究發現,反響迴路的興奮和抑制受大腦阿爾法節律(α-rhythm)調控,並在α-運動神經(α-motoneurones)中形成循環反饋系統(recurrent feedback system)。在二十世紀70-80年代,為模擬循環反饋系統而建立的各類數學模型為循環神經網路的發展奠定了基礎。
1982年,美國學者John Hopfield基於Little(1974)的神經數學模型使用二元節點建立了具有結合存儲(content-addressable memory)能力的神經網路,即Hopfield神經網路。Hopfield網路是一個包含外部記憶(external memory)的循環神經網路,其內部所有節點都相互連接,並使用能量函數進行學習。由於Hopfield (1982) 使用二元節點,因此在推廣至序列數據時受到了限制,但其工作受到了學界的廣泛關注,並啟發了其後的循環神經網路研究。
1986年,Michael I. Jordan基於Hopfield網路的結合存儲概念,在分散式并行處理(parallel distributed processing)理論下建立了新的循環神經網路,即Jordan網路。Jordan網路的每個隱含層節點都與一個“狀態單元(state units)”相連以實現延時輸入,並使用logistic函數(logistic function)作為激勵函數。Jordan網路使用反向傳播演演算法(Back-Probagation, BP)進行學習,並在測試中成功提取了給定音節的語音學特徵。之後在1990年,Jeffrey Elman提出了第一個全連接的循環神經網路,Elman網路。Jordan網路和Elman網路是最早出現的面向序列數據的循環神經網路,由於二者都從單層前饋神經網路出發構建遞歸連接,因此也被稱為簡單循環網路(Simple Recurrent Network, SRN)。
在SRN出現的同一時期,循環神經網路的學習理論也得到發展。在反向傳播演演算法的研究受到關注后,學界開始嘗試在BP框架下對循環神經網路進行訓練。1989年,Ronald Williams和David Zipser提出了循環神經網路的實時循環學習(Real-Time Recurrent Learning, RTRL)。隨後Paul Werbos在1990年提出了循環神經網路的隨時間反向傳播(BP Through Time,BPTT),RTRL和BPTT被沿用至今,是循環神經網路進行學習的主要方法。
1991年,Sepp Hochreiter發現了循環神經網路的長期依賴問題(long-term dependencies problem),即在對序列進行學習時,循環神經網路會出現梯度消失(gradient vanishing)和梯度爆炸(gradient explosion)現象,無法掌握長時間跨度的非線性關係。為解決長期依賴問題,大量優化理論得到引入並衍生出許多改進演演算法,包括神經歷史壓縮器(Neural History Compressor, NHC)、長短期記憶網路(Long Short-Term Memory networks, LSTM)、門控循環單元網路(Gated Recurrent Unit networks, GRU)、回聲狀態網路(echo state network)、獨立循環神經網路(Independent RNN)等。
在應用方面,SRN自誕生之初就被應用於語音識別任務,但表現並不理想,因此在二十世紀90年代早期,有研究嘗試將SRN與其它概率模型,例如隱馬爾可夫模型(Hidden Markov Model, HMM)相結合以提升其可用性。雙向循環神經網路(Bidirectional RNN, Bi-RNN)和雙向LSTM的出現提升了循環神經網路對自然語言處理的能力,但在二十世紀90年代,基於循環神經網路的有關應用沒有得到大規模推廣。二十一世紀后,隨著深度學習方法的成熟,數值計算能力的提升以及各類特徵學習(feature learning)技術的出現,擁有複雜構築的深度循環神經網路(Deep RNN, DRNN)開始在自然語言處理問題中展現出優勢,並成為語音識別、語言建模等應用的重要演演算法。
同在1997年,M. Schuster和K. Paliwal提出了具有深度結構的雙向循環神經網路(Bidirectional RNN, BRNN),並對其進行了語音識別試驗。雙向和門控構架的出現提升了RNN的學習表現,在一些綜述性研究中,被認為是RNN具有代表性的研究成果。
二十一世紀后,隨著深度學習理論的出現和數值計算能力的提升,擁有更高複雜度的RNN開始在自然語言處理問題中得到關注。2005年,Alex Graves等將雙向LSTM應用於語音識別,並得到了優於隱馬爾可夫模型(Hidden Markov Model, HMM)的表現。
2014年,K. Cho提出了門控循環單元網路(Gated Recurrent Unit networks, GRU),該方法是LSTM之後另一個受到關注的RNN門控構架。
2010年,Tomas Mikolov及其合作者提出了基於RNN的語言模型。2013-2015年, Y. Benjo、D. Bahdanau等提出了編碼器-解碼器、自注意力層等一系列RNN演演算法,並將其應用於機器翻譯問題。為語言模型設計的RNN演演算法在隨後的研究中啟發了包括Transformers、XLNet、ELMo、BERT等複雜構築
內部計算
全連接的循環單元
循環神經網路的核心部分是一個有向圖(directed graph)。有向圖展開中以鏈式相連的元素被稱為循環單元(RNN cell)。通常地,循環單元構成的鏈式連接可類比前饋神經網路中的隱含層(hidden layer),但在不同的論述中,循環神經網路的“層”可能指單個時間步的循環單元或所有的循環單元,因此作為一般性介紹,這裡避免引入“隱含層”的概念。給定按序列輸入的學習數據,循環神經網路的展開長度為。待處理的序列通常為時間序列,此時序列的演進方向被稱為“時間步(time-step)”。對時間步,循環神經網路的循環單元有如下表示:
式中稱為循環神經網路的系統狀態(system status),在動力系統的觀點下,系統狀態描述了一個給定空間中所有點隨時間步的變化。是內部狀態(internal status),與系統狀態有關。由於求解當前的系統狀態需要使用前一個時間步的內部狀態,因此循環單元的計算包含遞歸(recursion)。在樹結構的觀點下,所有先前時間步的循環單元都是當前時間步循環單元的父節點。式中是激勵函數或一個封裝的前饋神經網路,前者對應簡單循環網路(SRN),後者對應門控演演算法和一些深度演演算法。常見的激勵函數選擇包括logistic函數和雙曲正切函數(hyperbolic tangent function)。是循環單元內部的權重係數,與時間步無關,即對一組學習樣本,循環神經網路使用共享的權重計算所有時間步的輸出。
僅由循環單元構成的循環神經網路在理論上是可行的,但循環神經網路通常另有輸出節點,其定義為一個線性函數:
式中是權重係數。根據循環神經網路結構的不同,一個或多個輸出節點的計算結果在通過對應的輸出函數后可得到輸出值。例如對分類問題,輸出函數可以是歸一化指數函數(softmax function)或其它機器學習演演算法建立的分類器。
連接性
1.循環單元-循環單元連接:也被稱為“隱含-隱含連接(hidden-hidden connection)”或全連接,此時每個循環單元當前時間步的狀態由該時間步的輸入和上一個時間步的狀態決定:,是循環節點的權重,前者稱為狀態-狀態權重,後者稱為狀態-輸入權重。循環單元-循環單元連接可以是雙向的,對應雙向循環神經網路。
2.輸出節點-循環單元連接:該連接方式下循環單元的狀態由該時間步的輸入和上一個時間步的輸出(而不是狀態)決定: 。由於潛在假設了前一個時間步的輸出節點能夠表徵先前所有時間步的狀態,輸出節點-循環單元連接的循環神經網路不具有圖靈完備性,學習能力也低於全連接網路。但其優勢是可以使用Teacher Forcing進行快速學習。
3.基於上下文的連接:因為在圖網路的觀點下呈現閉環結構,該連接方式也被稱為閉環連接(closed-loop connection),其中循環單元的系統狀態引入了其上一個時間步的真實值。使用基於上下文連接的循環神經網路由於訓練時將學習樣本的真實值作為輸入,因此是一個可以逼近學習目標概率分佈的生成模型(generative model)。基於上下文的連接有多種形式,其中常見的一類使用了該時刻的輸入、上一時刻的狀態和真實值:。其它的類型可能使用固定長度的輸入,使用上一時刻的輸出代替真實值,或不使用該時刻的輸入。
通過建立輸出節點,循環神經網路可以有多種輸出模式,包括序列-分類器(單輸出)、序列-序列(同步多輸出)、編碼器-解碼器(非同步多輸出)等。
序列-分類器
序列-分類器的輸出模式適用於序列輸入和單一輸出的機器學習問題,例如文本分類(sentiment classification)。給定學習數據和分類標籤:,序列-分類器中循環單元的輸出節點會直接通過分類器,常見的選擇是使用最後一個時間步的輸出節點,或遞歸計算中所有系統狀態的均值。常見的序列-分類器使用全連接結構。
序列-序列
序列-序列的輸出模式中,序列的每個時間步對應一個輸出,即輸入和輸出的長度相同。給定學習目標,序列-序列的輸出模式在每個時間步都輸出結果。循環單元-循環單元連接、輸出節點-循環單元連接和基於上下文的連接都支持序列-序列輸出,其中前兩者常見於詞性標註(part-of-speech tagging)問題,後者可被應用於文本生成(text generation)和音樂合成(music composition)。
編碼器-解碼器(encoder-decoder)
在輸入數據和學習目標都為序列且長度可變時,可以使用兩個相耦合的基於上下文連接的循環神經網路,即編碼器-解碼器進行建模,編碼器-解碼器常被用於機器翻譯(Machine Translation, MT)問題,這裡以此為例進行說明。給定嵌入的原始文本和翻譯文本:,編碼器在工作時對原始文本進行處理,並輸出或到解碼器,解碼器根據編碼器的輸出生成新序列。編碼器-解碼器結構的循環神經網路以最大化為目標更新權重係數。
監督學習(supervised learning)
1. Teacher Forcing
Teacher Forcing是一種在序列-序列輸出模式下對循環神經網路進行快速訓練的方法,其理念是在每一個時間步的訓練中引入上一個時間步的學習目標(真實值)從而解耦誤差的反向傳播。具體地,Teacher Forcing是一種極大似然估計(Maximum Likelihood Estimation, MLE)方法,例如對序列的前兩個時間步,序列的對數似然有如下表示:
此時MLE將時間步的學習轉化為求解權重係數使的似然取極大值的優化問題,因此不需要將神經網路的誤差函數反向傳播至該時間步。
上述方法被稱為“嚴格的”Teacher Forcing,適用於輸出節點-循環單元連接的循環神經網路,對循環單元-循環單元連接的循環神經網路,只要輸出節點-循環單元可以連接,則Teacher Forcing可以和隨時間反向傳播(BPTT)一起使用。
嚴格的Teacher Forcing不適用於閉環連接的循環神經網路,因為該連接方式在測試時會將前一個時間步的輸出作為當前時間步的輸入,而Teacher Forcing在學習時使用的真實值和測試時神經網路自身的輸出往往有顯著差別。一個改進是對部分樣本進行自由學習,即使用神經網路自身的輸出代替真實的學習目標加入Teacher Forcing中。此外也可在Teacher Forcing的所有學習樣本中隨機混入,並隨著學習過程不斷增加混入的比例。
2. 隨時間反向傳播(BP Through Time, BPTT)
BPTT是反向傳播演演算法(BP)由前饋神經網路向循環神經網路的推廣,BPTT將循環神經網路的鏈式連接展開,其中每個循環單元對應一個“層”,每個層都按前饋神經網路的BP框架進行計算。考慮循環神經網路的參數共享性質,權重的梯度是所有層的梯度之和:式中為損失函數。這裡以循環單元-循環單元連接的多輸出網路為例介紹BPTT的計算步驟。首先給定如下的更新方程:式中需要求解的權重為。對最末端的時間步和其餘的時間步,求解總損失函數對循環單元狀態的偏導數是一組遞歸計算:由於循環神經網路參數共享,因此在計算當前時間步的梯度時需要將共享的參數對其它時間步的損失函數的變化“固定”,這裡使用“”表示該關係,在一些文獻中,該符號被稱為“實時導數(intermediate derivative)”。式中為激勵函數的導數,與輸出函數有關。按上式對所有時間步反向傳播后,循環神經網路的權重梯度更新按如下方式給出:
上述步驟為BPTT的標準求解框架,在理論上可以處理所有類型的循環神經網路。在實際應用中,由於損失函數對狀態的偏導數需要被完整地保存直到該樣本的所有參數更新完畢,因此在學習長序列樣本時,BPTT的空間複雜度顯著增加。對BPTT按固定長度截斷,即截斷的BPTT(truncated BPTT)可解決上述問題。
3. 實時循環學習(Real-Time Recurrent Learning, RTRL)
RTRL通過前向傳播的方式來計算梯度,在得到每個時間步的損失函數后直接更新所有權重係數至下一個時間步,類似於自動微分的前向連鎖(forward accumulation)模式。這裡以BPTT中的狀態-狀態權重為例做簡單介紹。在時間步,損失函數對權重中元素的實時更新規則如下:
其它權重的更新可以按相近的方式導出。相比於BPTT,RTRL的計算量更大,但因為無需存儲反向傳播的誤差梯度,RTRL的內存開銷更小,更適用於在線學習或使用長序列學習樣本的問題。
非監督學習(unsupervised learning)
使用編碼器-解碼器結構的循環神經網路能夠以自編碼器(Auto-Encoders, AE)的形式,即循環自編碼器(Recurrent AE)進行非監督學習。RAE是對序列數據進行特徵學習(feature learning)的方法之一,其工作方式與編碼器-解碼器相近。具體地,RAE輸入端的編碼器會處理序列並將最後一個時間步的狀態傳遞至解碼器,解碼器使用編碼器的輸出重構序列。RAE以最小化原始序列和重構序列的差異為目標進行學習。不同於一般的編碼器-解碼器結構,在學習完畢后,RAE只有編碼器部分會被取出使用,對輸入序列進行編碼。
非監督學習也可被應用於堆疊循環神經網路,其中最早被提出的方法是神經歷史壓縮器(Neural History Compressor, NHC)。NHC是一個自組織階層系統(self-organized hierarchical system),在學習過程中,NHC內的每個循環神經網路都以先前時間步的輸入 學習下一個時間步的輸入,學習誤差(通常由長距離依賴產生)會輸入到更高階層的循環神經網路中,在更長時間尺度下進行學習以。最終輸入數據會在NHC的各個階層得到完整的表徵,上述過程在研究中被描述為“壓縮(compression)”或“蒸餾(distillation)”。NHC在本質上是階層結構的AE,對輸入數據進行壓縮即是其特徵學習的過程。由於可以在多時間尺度上學習長距離依賴,因此NHC也被用於循環神經網路在監督學習問題中的預學習(pre-training)。
除上述方法外,循環神經網路有其它適用於特定問題的非監督學習方法。在對序列數據進行聚類(clustering)時,循環神經網路可以使用BINGO(Binary Information Gain Optimization)演演算法。對非參數學習問題,循環神經網路可以使用NEO(Non-parametric Entropy Optimization)演演算法。上述兩種演演算法使用較少,這裡不做贅述。
循環神經網路在誤差梯度在經過多個時間步的反向傳播后容易導致極端的非線性行為,包括梯度消失(gradient vanishing)和梯度爆炸(gradient explosion)。不同於前饋神經網路,梯度消失和梯度爆炸僅發生在深度結構中,且可以通過設計梯度比例得到緩解,對循環神經網路,只要序列長度足夠,上述現象就可能發生。在理解上,循環神經網路的遞歸計算類似於連續的矩陣乘法,例如 可視為一個不考慮激勵函數的循環神經網路,而該式實際等價於。由於循環神經網路使用固定的權重處理所有時間步,因此隨著時間步的推移,權重係數必然出現指數增長或衰減,引發梯度的顯著變化。
在實踐中,梯度爆炸雖然對學習有顯著影響,但較少出現,使用梯度截斷可以解決。梯度消失是更常見的問題且不易察覺,發生梯度消失時,循環神經網路在多個時間步后的輸出幾乎不與序列的初始值有關,例如先前式中的,因此無法模擬序列的長距離依賴(long-term dependency)。在數值試驗中,SRN對時間步跨度超過20的長距離依賴進行成功學習的概率接近於0。恰當的權重初始化(weight initialization),或使用非監督學習策略例如神經歷史壓縮器(NHC)可提升循環神經網路學習長距離依賴的能力,但對更一般的情形,循環神經網路發展了一系列優化策略,其中有很多涉及網路結構的改變和演演算法的改進。
梯度截斷
梯度截斷是處理循環神經網路梯度爆炸現象的有效方法,具體分為兩種,一是設定閾值並逐個元素篩查,若梯度超過閾值則截斷至閾值;二是在參數更新前,若誤差對參數的梯度超過閾值,則按范數(norm)截斷:
式中為梯度的閾值。比較可知,按范數截斷保持了截斷前後梯度的方向不變,因此邏輯上更合理,但試驗表明,兩種方法效果相當。事實上作為經驗方法,只要梯度截斷將權重係數帶離數值不穩定區域,就能很好地應對梯度爆炸現象。
正則化(regularization)
循環神經網路的正則化是應對其長距離依賴問題的方法之一,其理念是控制循環節點末端狀態對初始狀態導數,即雅可比矩陣的范數以提升循環神經網路對長距離誤差的敏感性。在誤差反向傳播至第個時間步時,其對應的正則化項有如下表示:
在BP中加入上述正則化項會顯著提升計算複雜度,此時可將包含損失函數的項近似為常數,並引導雅可比矩陣的范數向1靠近。研究表明,正則化和梯度截斷結合使用可以增加循環神經網路學習長距離依賴的能力,但相比於門控單元,正則化沒有減少模型的冗餘。
在前饋神經網路中被廣泛使用的隨機失活(dropout)策略也可用於循環神經網路。在輸入序列的維度大於1時,循環神經網路在每個時間步的輸入和狀態的矩陣元素都可以被隨機歸零:
式中為(0,1)-矩陣,也被稱為maxout矩陣(maxout array)隨機決定需要失活的連接。maxout矩陣可以對一組學習樣本的所有時間步保持不變,其中與系統狀態相乘的maxout矩陣也可隨時間步變化。在長序列的學習中,不斷生成隨機數進行隨機失活會降低演演算法的運行效率,一個可能的改進是假設距離過長的元素影響很小,並只對與當前時間步相隔一定範圍的循環單元連接使用隨機失活。
層歸一化(Layer Normalization, LN)
應用於循環神經網路時,LN將循環神經網路的每個循環單元視為一個層進行歸一化。對時間步,包含LN的循環節點的內部計算如下表示:
式中和為代表縮放和平移的參數,隨BP演演算法進行更新。在循環神經網路中,循環節點的均值和標準差會發生改變,產生協變漂移(covariate shift)現象,該現象會導致梯度爆炸和梯度消失,因此LN是緩解長距離依賴問題的方法之一。
儲層計算(reservoir computing)
儲層計算將循環神經網路中鏈式連接轉變為一個“儲層(reservoir)”,儲層內循環單元的狀態在每個時間步更新。儲層與輸出層相連,其對應的輸出權重由學習數據求解:
式中為儲層的輸入權重,在計算中隨機初始化並且固定,為輸出權重,按線性參數模型的計算方法求解。注意到上式中的遞歸是隨機的,因此儲層計算的構築本身緩解了循環神經網路的長距離依賴問題。同時,為確保儲層不發生梯度爆炸,其輸出權重有兩個重要設定:使用稀疏矩陣和特徵值的最大絕對值小於譜半徑(spectural radius)。譜半徑是一個超參數,用於控制 隨時間步的指數增長。稀疏矩陣控制儲層與輸出層間的鬆散連接,此時儲層中的信息只能在有限的輸出中“回聲”,不會擴散至網路的所有輸出中。
儲層計算可以被視為循環神經網路的學習理論或對循環神經網路的結構優化。使用儲層計算的循環神經網路包括回聲狀態網路(Echo State Network, ESN)和流體狀態機(liquid state machine),二者的不同點是流體狀態機的儲層單元是二元節點。儲層計算中隨機初始化並固定隱含層輸入權重的方法接近於極限學習機(Extreme Learning Machine, ELM),但後者基於前饋神經網路構建,其隱含層節點不是循環單元,不具有記憶性。
跳躍連接(skip connection)
梯度消失是時間步的函數,因此可以通過使用跳躍連接提高循環神經網路學習長距離依賴的能力。跳躍連接是跨多個時間步的長距離連接,引入跳躍連接后,長時間尺度的狀態能夠更好地在神經網路中傳遞,緩解梯度消失現象。有研究在使用跳躍連接的同時直接刪除循環單元-循環單元連接,強迫循環神經網路以階層結構在長時間尺度上運行。
滲漏單元(leaky unit)和門控單元(gated unit)
滲漏單元也被稱為線性自連接單元(linear self-connection unit)是在循環單元間模擬滑動平均(moving average)以保持循環神經網路中長距離依賴的方法:
式中的權重是預先給定的。由上式容易發現,滲漏單元會在迭代中優先記憶系統先前的狀態,因此提升了循環神經網路建立長期依賴的能力。研究表明ESN可以引入滲漏單元進行優化以提升其學習效果。
滲漏單元在應用中有兩個不足,一是人為給定的權重不是記憶系統狀態的最優方式,二是滲漏單元沒有遺忘功能,容易出現信息過載,在過去的狀態被循環單元充分使用后,將其遺忘可能是有利的。以此出發,門控單元是滲漏單元的推廣,門控單元的類型包括輸入門(input gate)、輸出門(output gate)和遺忘門(forget gate)。每個門都是一個封裝的神經網路,其計算方式可參見演演算法部分。總體而言,門控單元是減少學習誤差的長距離依賴的有效方法,使用門控單元的演演算法,包括長短期記憶網路(Long Short-Term Memory networks, LSTM)和門控循環單元網路(Gated Recurrent Unit networks, GRU)被證實在各類問題中有顯著優於SRN的表現。
簡單循環網路(Simple Recurrent Network, SRN)是僅包含一組鏈式連接(單隱含層)的循環神經網路,其中循環單元-循環單元連接的為Elman網路,閉環連接的為Jordan網路。對應的遞歸方式如下:式中和為激勵函數,例如邏輯斯蒂函數或雙曲正切函數。SRN在提出時使用BPTT進行監督學習,但不包含任何優化理論,因此無法學習長距離依賴,在現代的機器學習問題中很少直接使用。
門控演演算法是循環神經網路應對長距離依賴的重要方法,其思想是使用門控單元賦予循環神經網路控制其內部信息積累的能力,在學習時既能掌握長距離依賴又能選擇性地遺忘信息防止過載。門控演演算法使用BPTT和RTRL進行學習,其計算複雜度和學習表現均高於SRN。
長短期記憶網路(Long Short-Term Memory networks, LSTM)
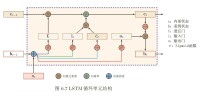
LSTM單元的內部結構
最初版本的LSTM沒有遺忘門,以全連接的方式進行序列-序列輸出,但本質上LSTM單元可以被引入其它各類循環神經網路構築中,例如LSTM自編碼器(LSTM Autoencoder)、堆疊LSTM(stacked LSTM)等。
對LSTM進行權重初始化時,需要為遺忘門設定較大的初始值,例如設定。過小的值會使得遺忘門在學習中快速遺忘先前時間步的信息,不利於神經網路學習長距離依賴,並可能導致梯度消失。
門控循環單元網路(Gated Recurrent Unit networks, GRU)
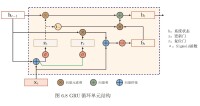
GRU的內部結構
LSTM和GRU有很多變體,包括在循環單元間共享更新門和複位門參數,以及對整個鏈式連接使用全局門控,但研究表明這些改進版本相比於標準演演算法未體現出明顯優勢,其可能原因是門控演演算法的表現主要取決於遺忘門,而上述變體和標準演演算法使用了的遺忘門機制相近。
循環神經網路的“深度”包含兩個層面,即序列演進方向的深度和每個時間步上輸入與輸出間的深度。對前者,循環神經網路的深度取決於其輸入序列的長度,因此在處理長序列時可以被認為是直接的深度網路;對後者,循環神經網路的深度取決於其鏈式連接的數量,單鏈的循環神經網路可以被認為是“單層”的。
循環神經網路能夠以多種方式由單層加深至多層,其中最常見的策略是使用堆疊的循環單元。由於在序列演進方向已經存在複雜結構,因此不同於深度的前饋神經網路,深度循環神經網路在輸入和輸出間不會堆疊太多層次,一個3層的深度循環神經網路已經具有很大規模。
堆疊循環神經網路(Stacked Recurrent Neural Network, SRNN)
SRNN是在全連接的單層循環神經網路的基礎上堆疊形成的深度演演算法。SRNN內循環單元的狀態更新使用了其前一層相同時間步的狀態和當前層前一時間步的狀態:
式中符號含義參見循環單元部分,上標分別表示時間步和層數。參與構建SRNN的循環神經網路可以是簡單循環網路(SRN)或門控演演算法。使用SRN構建的SRNN也被稱為循環多層感知器(Recurrent Multi-Layer Perceptron,RMLP),是1991年被提出的深度循環神經網路。
雙向循環神經網路(bidirectional recurrent neural network, Bi-RNN)
Bi-RNN是兩層的深度循環神經網路,被應用於學習目標與完整(而不是截止至當前時間步)輸入序列相關的場合。例如在語音識別中,當前語音對應的辭彙可能與其後出現的辭彙有對應關係,因此需要以完整的語音作為輸入。Bi-RNN的兩個鏈式連接按相反的方向遞歸,輸出的狀態會進行矩陣拼接並通過輸出節點,其更新規則如下:
式中符號含義參見循環單元部分,表示矩陣拼接。和SRNN類似,Bi-RNN也可以由各種類型的循環單元構成,例如由LSTM構成的版本被稱為雙向LSTM。
外部記憶
循環神經網路在處理長序列時有信息過載的問題,例如對編碼器-解碼器結構,編碼器末端的輸出可能無法包含序列的全部有效信息。門控演演算法的遺忘門/更新門可以有選擇地丟棄信息,減緩循環單元的飽和速度,但更進一步地,有研究通過將信息保存在外部記憶(external memory)中,並在需要時再進行讀取,以提高循環神經網路的網路容量(network capacity)。使用外部記憶的循環神經網路包括神經圖靈機(Neural Turing Machine, NTM)、Hopfield神經網路等。
與卷積神經網路相結合
循環神經網路與卷積神經網路相結合的常見例子是循環卷積神經網路(Recurrent CNN, RCNN)。RCNN將卷積神經網路的卷積層替換為內部具有遞歸結構的循環卷積層(Recurrent Convolutional Layer, RCL),並按前饋連接建立深度結構。
除RCNN外,循環神經網路和卷積神經網路還可以通過其它方式相結合,例如使用卷積神經網路對序列化的格點輸入進行特徵學習,並將結果按輸入循環神經網路。
遞歸神經網路和圖網路
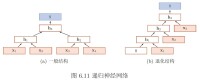
一般的遞歸神經網路(左),結構退化后的循環神經網路(右)
遞歸神經網路是循環神經網路由鏈式結構向樹狀結構的推廣。不同於循環神經網路的鏈式連接,遞歸神經網路的每個子節點都可以和多個父節點相連並傳遞狀態。當其所有子節點都僅與一個父節點相連時,遞歸神經網路退化為循環神經網路。遞歸神經網路的節點可加入門控機制,例如通過LSTM門控得到樹狀長短期記憶網路(tree-structured LSTM)。圖網路是循環神經網路和遞歸神經網路的進一步推廣,或者說后兩者是圖網路在特定結構下的神經網路實現。在圖網路觀點下,全連接的循環神經網路是一個有向無環圖,而上下文連接的循環神經網路是一個有向環圖。遞歸神經網路和圖網路通常被用於學習數據具有結構關係的場合,例如語言模型中的語法結構。
權重共享:循環神經網路的權重係數是共享的,即在一次迭代中,循環節點使用相同的權重係數處理所有的時間步。相比於前饋神經網路,權重共享顯著降低了循環神經網路的總參數量,增強了網路的泛化能力。同時,權重共享也意為著循環神經網路可以提取序列中隨時間變化的動力特徵,因此其在學習和測試序列具有不同長度時也可以有穩定的表現。
計算能力:可以證明,一個循環單元間完全連接的循環神經網路滿足通用近似定理,即全聯接循環神經網可以按任意精度逼近任意非線性系統,且對狀態空間的緊緻性沒有限制,只要其擁有足夠多的非線性節點。在此基礎上,任何圖靈可計算函數(Turing computable function)都可以由有限維的全聯接循環神經網路計算,因此循環神經網路是圖靈完備(Turing completeness)的。
作為時間序列模型的性質:在時間序列建模的觀點下,循環神經網路是一個無限衝激響應濾波器(Infinite Impulse Response filter, IIR)。這將循環神經網路與其它應用於序列數據的權重共享模型,例如一維的卷積神經網路相區分,後者以時間延遲網路為代表,是有限衝激響應濾波器(Finite Impulse Response filter, FIR)。
自然語言數據是典型的序列數據,因此處理序列數據具有內在優勢的循環神經網路是各類NLP問題的重要演演算法。在語音識別(speech recognition)中,循環神經網路被廣泛應用於端到端(end-to-end)建模,例如有研究使用LSTM單元構建的雙向深度循環神經網路成功進行了英語文集TIMIT的語音識別,其識別準確率超過了同等條件的隱馬爾可夫模型(Hidden Markov Model, HMM)和深度前饋神經網路。
循環神經網路是機器翻譯(Machine Translation, MT)的主流演演算法之一,並形成了區別於“統計機器翻譯”的“神經機器翻譯(neural machine translation)”方法。有研究使用端到端學習的LSTM成功對法語-英語文本進行了翻譯,也有研究將卷積n元模型(convolutional n-gram model)與循環神經網路相結合進行機器翻譯。有研究認為,按編碼器-解碼器形式組織的LSTM能夠在翻譯中考慮語法結構。
基於上下文連接的循環神經網路,被大量用語言建模(language modeling)問題。有研究在字元層面(character level)的語言建模中,將循環神經網路與卷積神經網路相結合併取得了良好的學習效果。循環神經網路也是語義分析( sentiment analysis)的工具之一,被應用於文本分類、社交網站數據挖掘 等場合。
在語音合成(speech synthesis)領域,有研究將多個雙向LSTM相組合建立了低延遲的語音合成系統,成功將英語文本轉化為接近真實的語音輸出。循環神經網路也被用於端到端文本-語音(Text-To-Speech, TTS)合成工具的開發,例子包括Tacotron、Merlin 等。
循環神經網路與卷積神經網路向結合的系統在計算機視覺問題中有一定應用,例如在字元識別(text recognition)中,有研究使用卷積神經網路對包含字元的圖像進行特徵提取,並將特徵輸入LSTM進行序列標註。對基於視頻的計算機視覺問題,例如行為認知(action recognition)中,循環神經網路可以使用卷積神經網路逐幀提取的圖像特徵進行學習。
在計算生物學(computational biology)領域,深度循環神經網路被用於分析各類包含生物信息的序列數據,有關主題包括在DNA序列中識別分割外顯子(exon)和內含子(intron)的斷裂基因(split gene)、通過RNA序列識別小分子RNA(microRNA)、使用蛋白質序列進行蛋白質亞細胞定位(subcellular location of proteins)預測 等。
在地球科學(earth science)領域,循環神經網路被用於時間序列變數的建模和預測。使用LSTM建立的水文模型(hydrological model)對土壤濕度的模擬效果與陸面模式相當。而基於LSTM的降水-徑流模式(rainfall-runoff model)所輸出的徑流量與美國各流域的觀測結果十分接近。在預報方面,有研究將地面遙感數據作為輸入,使用循環卷積神經網路進行單點降水的臨近預報(nowcast)。
包含循環神經網路的編程模塊
現代主流的機器學習庫和界面,包括TensorFlow、Keras、Thenao、Microsoft-CNTK等都支持運行循環神經網路。此外有基於特定數據的循環神經網路構建工具,例如面向音頻數據開發的auDeep 等。