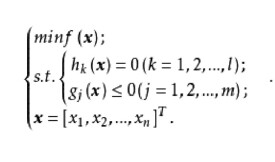約束條件
約束條件
在數學規劃中,對於決策方案的各項限制,常以不等式或方程式的形式出現。在經濟問題中,對目標函數常常要在一定約束條件下求最大值(或最小值),它們包含著用來代表決策方案的變數,藉以對決策方案施加限制範圍。
運用單純形法解某些線性規劃問題時,該問題已知的並須遵守的前提條件稱為約束條件。
約束條件:
…………………………
式中x1,x2,…,xn為企業生產的各種產品;b1,b2,…,bm為可供使用的各種投入要素的數量;為第j種產品每生產1個單位所需要的第i種投入要素的數量;最後,非負值約束條件表示各種產品的產量必須是正值,負值是沒有意義的。
在優化設計中,目標函數取決於設計變數,而設計變數的取值範圍都有各種限制條件,如強度、剛度等。每個限制條件都可寫成包含設計變數的函數,稱為約束條件或設計約束。因為它是設計變數的函數,也稱為約束函數。
約束函數可用等式或不等式描述。如果約束函數能夠反映設計變數之間明顯的函數關係,稱為顯式約束;否則,稱為隱式約束。
等式約束是對設計變數的嚴格約束,起著降低設計自由度的作用,其形式為:
式中, l為等式約束的數目,n為設計維數。
在機械優化設計中,大部分約束為不等式約束,其形式為:
式中,m為不等式約束的數目。根據約束的性質,分為幾何約束(邊界約束)和性能約束。
幾何約束:根據某種設計要求,設計變數必須滿足的某些幾何條件以及只對設計變數的取值範圍加以限制的那些約束,如桿的長度、桿的橫截面積等。
性能約束:指滿足特定工作性能而建立的約束條件,如工作應力小於許用應力等。
對於等式約束而言,設計變數所代表的設計點必須在 所表示的面(或線)上,稱為起作用約束或緊約束。對於不等式約束,極限情況 所表示的幾何面或線將設計空間分成兩部分:一部分中所有設計均滿足所有的約束條件,這部分空間稱為設計點的可行域;另一部分所有點均不滿足約束條件,稱為設計點的不可行域。在可行域內的設計點,稱為可行設計點,可行域也是可行設計點的集合。位於可行域邊界上的設計點亦是可行點,過該點的約束為起作用約束,否則為不起作用約束;非可行域是不滿足約束條件設計點的集合。
設計變數
在設計中不斷變化,能夠獨立影響設計目標的設計參數稱為設計變數,一般用列向量或行向量的轉置表示。設 為優化設計中的n個變數,記為或把定義為門維歐式空間 的一個列向量,該空間包含了設計中所有可能的設計方案,且每一個設計方案對應設計空間上的一個設計向量或者一個設計點。設計變數的個數行稱為設計問題的維數,有幾個設計變數就稱為幾維優化設計問題。設計問題的維數表徵了設計自由度。自由度越大,越有利於尋找最理想的設計方案,但設計的難度也越大。
n=2就是一個二維設計問題,可以用直角坐標系表示,也稱平面設計問題;n=3是一個三維設計問題,可用三個坐標軸所構成的直角坐標系表示,也稱三維設計空間;n>3時為抽象的超空間,無法用圖形表示。
在設計域中,按變數是否連續分為連續變數(如構件尺寸、轉速等)和離散變數(如齒輪的齒數等)。按變數的性質分為幾何參數、物理參數和力學參數等,如桿的截面積、長度等即為幾何參數,桿的質量、彈性模量和泊松比為物理參數,桿的應力、應變等為力學參數等。
根據設計變數維數的多少,優化設計問題可以分為小型優化設計問題、中型優化設計問題和大型優化設計問題(n>50)等。
目標函數
為了對設計進行評價,必須構造包含設計變數的評價函數,即優化的目標,稱為目標函數,一般以表示。
在優化過程中,通過設計變數的改變不斷改善 的值,最後求得令 值最好或最滿意的x值。在目標函數的構造中,應注意目標函數必須包含全部設計變數。
目標函數一般用極小值表示,即,若求目標函數的極大值,一般用 轉換為極小值問題,因此極大化和極小化都可統一表示為求極小,即在機械設計中,一般用作目標函數的有體積最小、質量最小、效率最大、柔度最小、振幅或雜訊最小、成本最低,等等。
機械優化設計一般分為單目標優化問題和多目標優化問題。只有一個目標函數的優化問題稱為單目標優化問題;在同一個設計中要提出多個目標區數時,稱為多目標優化問題。目標函數愈多,設計的綜合效果愈好,但求解的難度也愈大。