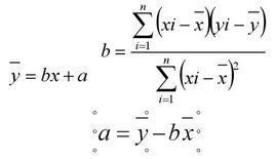提到回歸直線,首先要知道變數的相關性。變數與變數之間的關係常見的有兩類:一類是確定性的函數關係,像正方形的邊長a和面積S的關係;另一類是變數間確實存在關係,但又不具備函數關係所要求的確定性,它們的關係是隨機性的。當兩個相互關係的量具有這兩種變數關係的時候,就稱兩個變數具有相關關係。
在此基礎上,可以畫出y隨x變化的圖形,將已知的數據在所作的直角坐標系中進行描點。這樣的圖形叫做散點圖。
回歸直線方程是根據樣本資料通過回歸分析所得到的反映一個變數(因變數)對另一個或一組變數(
自變數)的回歸關係的數學表達式。指在一組具有相關關係的變數的數據(x與Y)間,一條最好地反映x與Y之間的關係直線。
離差作為表示xi對應的回歸直線縱坐標y與觀察值yi的差,其幾何意義可用點與其在回歸直線豎直方向上的投影間的距離來描述。數學表達:.總離差不能用n個離差之和來表示,通常是用離差的平方和即計算。
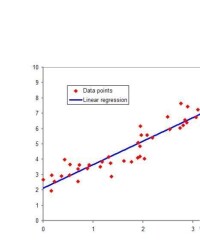
回歸直線
如果散點圖中點的分佈從整體看大致在一條直線附近,我們就稱這兩個變數之間具有線性相關關係,這條直線叫做回歸直線。根據不同的標準,可以畫出不同的直線來近似表示這種線性相關關係。比如可以連接最左側點和最右側點得到一條直線,或者讓畫出的直線上方的點和下方的點數目相等。當所有數據點都分佈在一條直線附近,顯然這樣的直線還可以畫出許多條,而我們希望找出其中的一條,它能最好地反映x與Y的關係,換言之,我們要找出一條直線,使這條直線“最貼近”已知的數據點。記此直線方程為。這裡在y的上方加記號“^”是為了區分Y的實際值y,表示x取值時,Y相應的觀察值為yi,而直線上對應於xi的縱坐標是(i為x右下角的數值)。式叫做Y對x的回歸直線方程,b叫
回歸係數。要確定回歸直線方程,只要確定a與回歸係數b。
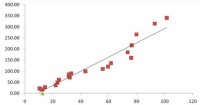
回歸直線
在
回歸分析中,用來描述具有
線性關係的因變數y與自變數xi的關係曲線,其一般表達式是。
“
回歸”這個詞是由
英國著名的
統計學家 Francils Galton 提出來的。1889年,他在研究祖先與後代身高之間的關係時發現,身材較高的父母,他們的孩子也較高,但這些孩子的平均身高並沒有他們父母的平均身高高;身材較矮的父母,他們的孩子也較矮,但這些孩子的平均身高卻比他們父母平均身高高。Galton 把這種後代的身高向中間值靠近的趨勢稱為“回歸現象”。後來,人們把由一個變數的變化去推測另一個變數的變化的方法叫做回歸方法。