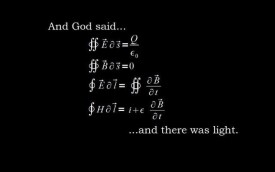麥克斯韋方程組

麥克斯韋誕生前的半個多世紀，人類對電磁現象的認識取得了很大的進展。1785年，法國物理學家C. A.庫侖（Charles A. Coulomb）在扭秤實驗結果的基礎上，建立了說明兩個點電荷之間相互作用力的庫侖定律。1820年，H. C.奧斯特（Hans Christian Oersted）發現電流能使磁針偏轉，從而把電與磁聯繫起來。其後，A. M.安培（Andre Marie Ampère）研究了電流之間的相互作用力，提出了許多重要概念和安培環路定律。M.法拉第（Michael Faraday）在很多方面有傑出貢獻，特別是1831年發表的電磁感應定律，是電機、變壓器等設備的重要理論基礎。

1845年，關於電磁現象的三個最基本的實驗定律：庫侖定律（1785年）、畢奧-薩伐爾定律（1820年）、法拉第電磁感應定律（1831 ~ 1845年）已被總結出來，法拉第的“電力線”和“磁力線”（現在也叫做“電場線”與“磁感線”）概念已發展成“電磁場概念”。1855年至1865年，麥克斯韋在全面地審視了庫侖定律、畢奧—薩伐爾定律和法拉第定律的基礎上，把數學分析方法帶進了電磁學的研究領域，由此導致麥克斯韋電磁理論的誕生。

在麥克斯韋之前，關於電磁現象的學說都以超距作用觀念為基礎，認為帶電體、磁化體或載流導體之間的相互作用，都是可以超越中間媒質而直接進行並立即完成的，即認為電磁擾動的傳播速度無限大。在那個時期，持不同意見的只有法拉第。他認為上述這些相互作用與中間媒質有關，是通過中間媒質的傳遞而進行的，即主張間遞學說。

麥克斯韋繼承了法拉第的觀點，參照流體力學的模型，應用嚴謹的數學形式總結了前人的工作，提出了位移電流的假說，推廣了電流的涵義，將電磁場基本定律歸結為四個微分方程，這就是著名的麥克斯韋方程組。他對這組方程進行了分析，預見到電磁波的存在，並斷定，電磁波的傳播速度為有限值（與光速接近），且光也是某種頻率的電磁波。上述這些，他都寫入題為《論電與磁》的論文中。

1887年，海因里希·魯道夫·赫茲（Heinrich R. Hertz）用實驗方法產生和檢測到了電磁波，證實了麥克斯韋的預見。1905～1915年間，A.愛因斯坦（Albert Einstein）的相對論進一步論證了時間、空間、質量、能量和運動之間的關係，說明電磁場就是物質的一種形式，間遞學說得到了公認。

麥克斯韋方程組乃是由四個方程共同組成的：

● ● 高斯定律：該定律描述電場與空間中電荷分佈的關係。電場線開始於正電荷，終止於負電荷（或無窮遠）。計算穿過某給定閉曲面的電場線數量，即其電通量，可以得知包含在這閉曲面內的總電荷。更詳細地說，這定律描述穿過任意閉曲面的電通量與這閉曲面內的電荷之間的關係。

● ● 高斯磁定律：該定律表明，磁單極子實際上並不存在。所以，沒有孤立磁荷，磁場線沒有初始點，也沒有終止點。磁場線會形成循環或延伸至無窮遠。換句話說，進入任何區域的磁場線，必需從那區域離開。以術語來說，通過任意閉曲面的磁通量等於零，或者，磁場是一個無源場。

● ● 法拉第感應定律：該定律描述時變磁場怎樣感應出電場。電磁感應是製造許多發電機的理論基礎。例如，一塊旋轉的條形磁鐵會產生時變磁場，這又接下來會生成電場，使得鄰近的閉合電路因而感應出電流。

● ● 麥克斯韋-安培定律：該定律闡明，磁場可以用兩種方法生成：一種是靠傳導電流（原本的安培定律），另一種是靠時變電場，或稱位移電流（麥克斯韋修正項）。

在電磁學里，麥克斯韋修正項意味著時變電場可以生成磁場，而由於法拉第感應定律，時變磁場又可以生成電場。這樣，兩個方程在理論上允許自我維持的電磁波傳播於空間。

麥克斯韋電磁場理論的要點可以歸結為：

①幾分立的帶電體或電流，它們之間的一切電的及磁的作用都是通過它們之間的中間區域傳遞的，不論中間區域是真空還是實體物質。

②電能或磁能不僅存在於帶電體、磁化體或帶電流物體中，其大部分分佈在周圍的電磁場中。

③導體構成的電路若有中斷處，電路中的傳導電流將由電介質中的位移電流補償貫通，即全電流連續。且位移電流與其所產生的磁場的關係與傳導電流的相同。

④磁通量既無始點又無終點，即不存在磁荷。

⑤光波也是電磁波。

麥克斯韋方程組有兩種表達方式。

1. 積分形式的麥克斯韋方程組是描述電磁場在某一體積或某一面積內的數學模型。表達式為：

式①是由安培環路定律推廣而得的全電流定律，其含義是：磁場強度H沿任意閉合曲線的線積分，等於穿過此曲線限定面積的全電流。等號右邊第一項是傳導電流．第二項是位移電流。式②是法拉第電磁感應定律的表達式，它說明電場強度E沿任意閉合曲線的線積分等於穿過由該曲線所限定面積的磁通對時間的變化率的負值。這裡提到的閉合曲線，並不一定要由導體構成，它可以是介質迴路，甚至只是任意一個閉合輪廓。式③表示磁通連續性原理，說明對於任意一個閉合曲面，有多少磁通進入曲面就有同樣數量的磁通離開。即B線是既無始端又無終端的；同時也說明並不存在與電荷相對應的磁荷。式④是高斯定律的表達式，說明在時變的條件下，從任意一個閉合曲面出來的D的凈通量，應等於該閉曲面所包圍的體積內全部自由電荷之總和。

2. 微分形式的麥克斯韋方程組。微分形式的麥克斯韋方程是對場中每一點而言的。應用del運算元，可以把它們寫成

式⑤是全電流定律的微分形式，它說明磁場強度H的旋度等於該點的全電流密度（傳導電流密度J與位移電流密度之和），即磁場的漩渦源是全電流密度，位移電流與傳導電流一樣都能產生磁場。式⑥是法拉第電磁感應定律的微分形式，說明電場強度E的旋度等於該點磁通密度B的時間變化率的負值，即電場的渦旋源是磁通密度的時間變化率。式⑦是磁通連續性原理的微分形式，說明磁通密度B的散度恆等於零，即B線是無始無終的。也就是說不存在與電荷對應的磁荷。式⑧是靜電場高斯定律的推廣，即在時變條件下，電位移D的散度仍等於該點的自由電荷體密度。

除了上述四個方程外，還需要有媒質的本構關係式

才能最終解決場量的求解問題。式中ε是媒質的介電常數，μ是媒質的磁導率，σ是媒質的電導率。

一般形式

麥克斯韋方程組的積分形式如下：

這是1873年前後，麥克斯韋提出的表述電磁場普遍規律的四個方程。其中：

（1）描述了電場的性質。在一般情況下，電場可以是自由電荷的電場也可以是變化磁場激發的感應電場，而感應電場是渦旋場，它的電位移線是閉合的，對封閉曲面的通量無貢獻。

（2）描述了磁場的性質。磁場可以由傳導電流激發，也可以由變化電場的位移電流所激發，它們的磁場都是渦旋場，磁感應線都是閉合線，對封閉曲面的通量無貢獻。

（3）描述了變化的磁場激發電場的規律。

（4）描述了傳導電流和變化的電場激發磁場的規律。

穩恆場中的形式

當

時，方程組就還原為靜電場和穩恆磁場的方程：

無場源自由空間中的形式

當，方程組就成為如下形式：

麥克斯韋方程組的積分形式反映了空間某區域的電磁場量(D、E、B、H)和場源(電荷q、電流I)之間的關係。

在電磁場的實際應用中，經常要知道空間逐點的電磁場量和電荷、電流之間的關係。從數學形式上，就是將麥克斯韋方程組的積分形式化為微分形式。

國際單位制下的形式

注意：

(1)在不同的慣性參照系中，麥克斯韋方程組有同樣的形式。

(2) 應用麥克斯韋方程組解決實際問題，還要考慮介質對電磁場的影響。例如在均勻各向同性介質中，電磁場量與介質特性量有下列關係：

在非均勻介質中，還要考慮電磁場量在界面上的邊值關係。在利用t=0時場量的初值條件，原則上可以求出任一時刻空間任一點的電磁場，即E(x,y,z,t)和B(x,y,z,t)。

高斯單位制下的形式

對於正弦時變場，可以使用復矢量將電磁場定律表示為複數形式。

在複數形式的電磁場定律中，由於複數場量和源量都只是空間位置的函數，在求解時，不必再考慮它們與時間的依賴關係。因此，對討論正弦時變場來說面採用複數形式的電磁場定律是較為方便的。

採用不同的單位制，麥克斯韋方程組的形式會稍微有所改變，大致形式仍舊相同，只是不同的常數會出現在方程內部不同位置。

國際單位制是最常使用的單位制，整個工程學領域都採用這種單位制，大多數化學家也都使用這種單位制，大學物理教科書幾乎都採用這種單位制。其它常用的單位制有高斯單位制、洛倫茲-赫維賽德單位制（Lorentz-Heaviside units）和普朗克單位制。由厘米-克-秒制衍生的高斯單位制，比較適合於教學用途，能夠使得方程看起來更簡單、更易懂。洛倫茲-赫維賽德單位制也是衍生於厘米-克-秒制，主要用於粒子物理學；普朗克單位制是一種自然單位制，其單位都是根據自然的性質定義，不是由人為設定。普朗克單位制是研究理論物理學徠非常有用的工具，能夠給出很大的啟示。在本頁里，除非特別說明，所有方程都採用國際單位制。

這裡展示出麥克斯韋方程組的兩種等價表述。第一種表述如下：

這種表述將自由電荷和束縛電荷總和為高斯定律所需要的總電荷，又將自由電流、束縛電流和電極化電流總合為麥克斯韋-安培定律內的總電流。這種表述採用比較基礎、微觀的觀點。這種表述可以應用於計算在真空里有限源電荷與源電流所產生的電場與磁場。但是，對於物質內部超多的電子與原子核，實際而言，無法一一納入計算。事實上，經典電磁學也不需要這麼精確的答案。

第二種表述見前所述”積分形式“中的”一般形式“。它以自由電荷和自由電流為源頭，而不直接計算出現於電介質的束縛電荷和出現於磁化物質的束縛電流和電極化電流所給出的貢獻。由於在一般實際狀況，能夠直接控制的參數是自由電荷和自由電流，而束縛電荷、束縛電流和電極化電流是物質經過極化后產生的現象，採用這種表述會使得在介電質或磁化物質內各種物理計算更加簡易。

表面上看，麥克斯韋方程組似乎是超定的（overdetermined）方程組，它只有六個未知量（矢量電場、磁場各擁有三個未知量，電流與電荷不是未知量，而是自由設定並符合電荷守恆的物理量），但卻有八個方程（兩個高斯定律共有兩個方程，法拉第定律與安培定律是矢量式，各含有三個方程）。這狀況與麥克斯韋方程組的某種有限重複性有關。從理論可以推導出，任何滿足法拉第定律與安培定律的系統必定滿足兩個高斯定律。

另一方面，麥克斯韋方程組又是不封閉的。只有給定了電磁介質的特性，此方程組才能得到定解。

麥克斯韋方程組通常應用於各種場的“宏觀平均場”。當尺度縮小至微觀（microscopic scale），以至於接近單獨原子大小的時侯，這些場的局部波動差異將變得無法忽略，量子現象也會開始出現。只有在宏觀平均的前提下，一些物理量如物質的電容率和磁導率才會得到有意義的定義值。

最重的原子核的半徑大約為7飛米（ ）。所以，在經典電磁學里，微觀尺度指的是尺寸的數量級大於。滿足微觀尺度，電子和原子核可以視為點電荷，微觀麥克斯韋方程組成立；否則，必需將原子核內部的電荷分佈納入考量。在微觀尺度計算出來的電場與磁場仍舊變化相當劇烈，空間變化的距離數量級小於 米，時間變化的周期數量級在10至10秒之間。因此，從微觀麥克斯韋方程組，必需經過經典平均運算，才能得到平滑、連續、緩慢變化的宏觀電場與宏觀磁場。宏觀尺度的最低極限為10米。這意味著電磁波的反射與折射行為可以用宏觀麥克斯韋方程組來描述。以這最低極限為邊長，體積為10立方米的立方體大約含有10個原子核和電子。這麼多原子核和電子的物理行為，經過經典平均運算，足以平緩任何劇烈的漲落。根據可靠文獻記載，經典平均運算只需要在空間作平均運算，不需要在時間作平均運算，也不需要考慮到原子的量子效應。[5]

8評價

編輯

麥克斯韋方程組在電磁學中的地位，如同牛頓運動定律在力學中的地位一樣。以麥克斯韋

方程組為核心的電磁理論，是經典物理學最引以自豪的成就之一。它所揭示出的電磁相互作用的完美統一，為物理學家樹立了這樣一種信念：物質的各種相互作用在更高層次上應該是統一的。這個理論被廣泛地應用到技術領域。

麥克斯韋方程組

(一)經典場論是19世紀後期麥克斯韋在總結電磁學三大實驗定律並把它與力學模型進行類比的基礎上創立起來的。但麥克斯韋的主要功績恰恰使他能夠跳出經典力學框架的束縛：在物理上以"場"而不是以"力"作為基本的研究對象，在數學上引入了有別於經典數學的矢量偏微分運算符。這兩條是發現電磁波方程的基礎。這就是說，實際上麥克斯韋的工作已經衝破經典物理學和經典數學的框架，只是由於當時的歷史條件，人們仍然只能從牛頓的經典數學和力學的框架去理解電磁場理論。

現代數學，Hilbert空間中的數學分析是在19世紀與20世紀之交的時候才出現的。而量子力學的物質波的概念則在更晚的時候才被發現，特別是對於現代數學與量子物理學之間的不可分割的數理邏輯聯繫至今也還沒有完全被人們所理解和接受。從麥克斯韋建立電磁場理論到如今，人們一直以歐氏空間中的經典數學作為求解麥克斯韋方程組的基本方法。

(二) 我們從麥克斯韋方程組的產生，形式，內容和它的歷史過程中可以看到：第一，物理對象是在更深的層次上發展成為新的公理表達方式而被人類所掌握，所以科學的進步不會是在既定的前提下演進的，一種新的具有認識意義的公理體系的建立才是科學理論進步的標誌。第二，物理對象與對它的表達方式雖然是不同的東西，但如果不依靠合適的表達方法就無法認識到這個對 象的“存在”。第三，我們正在建立的理論將決定到我們在何種層次的意義上使我們的對象成為物理事實,，這正是現代最前沿的物理學所給我們帶來的困惑。

(三) 麥克斯韋方程組揭示了電場與磁場相互轉化中產生的對稱性優美，這種優美以現代數學形式得到充分的表達。但是，我們一方面應當承認，恰當的數學形式才能充分展示經驗方法中看不到的整體性(電磁對稱性)；另一方面，我們也不應當忘記，這種對稱性的優美是以數學形式反映出來的電磁場的統一本質。因此，我們應當認識到應在數學的表達方式中"發現"或"看出" 了這種對稱性，而不是從物理數學公式中直接推演出這種本質。