自由沉降
自由沉降
單個礦粒在廣闊的介質空間中的獨自沉降稱作自由沉降,在自由沉降過程中,礦粒只受到本身重力、介質浮力和阻力的作用而不受其他因素影響。當粒群中顆粒之間的距離較大,也就是體積濃度(礦粒所佔的總體積與懸浮體總容積之比)很小時(一般小於3%),礦粒之間的干涉作用變得很弱,此時可視為自由沉降。
靜止顆粒因重力而下沉,逐漸加速。此為沉降的加速階段。
沉降中的顆粒受到周邊液體的阻力.沉降加快時,所受到的阻力也增大,加速度逐漸減小。當重力和阻力相等時加速度降為零,顆粒恆速下降。該速度稱為終端速度。這是小顆粒沉降與自由落體的區別之處。物理學中討論自由落體時,忽略空氣的阻力,因此,自由落體是以恆定的加速度(重力加速度)下降。小顆粒沉降時,顆粒的相對錶面積很大,阻力不容忽略,從而導致恆速階段的出現。這是顆粒沉降的重要特點。顆粒愈小,加速階段愈短,恆速階段出現得愈早。因此,對於細小的顆粒,甚至可以忽略加速階段,將顆粒沉降過程視為恆速沉降過程,並將該終端速度稱為沉降速度。
流體對固體顆粒做繞流運動時,在流動方向上對顆粒施加一個曳力。曳力與流體的密度ρ、黏度μ、流動速度u有關,而且受顆粒的形狀與定向的影響,問題較為複雜。只有幾何形狀簡單的少數例子可以獲得曳力的理論計算式。
對光滑圓球,曳力採用下式計算:
若令
式(1)可作為曳力係數的定義式。
曳力係數與顆粒雷諾數的關係經實驗測定示於下圖中。
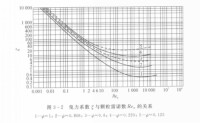
曳力係數與顆粒雷諾數的關係
設想將表面光滑的球形顆粒置於靜止的粘性流體介質中,如果顆粒的密度大於流體的密度,顆粒將在流體中做下沉運動。此時,顆粒將受到重力、浮力和阻力的作用。重力向下,浮力向上,阻力是顆粒表面與流體摩擦時產生的,是流體介質對顆粒實施拖曳的力,與顆粒運動方向相反,因此作用方向是向上的。重力減去浮力和阻力,是促使顆粒沉降的凈力。在此力的作用下,顆粒產生一定的加速度。隨著顆粒沉降速度的增加,阻力增大。當阻力增大到等於重力與浮力之差時,顆粒受到的合力為零。此後顆粒便以加速度為零的瞬時速度等速向下運動。
由此可見,顆粒在靜止的粘性流體中沉降有兩個階段。第一階段為加速段。此時顆粒受到其值等於重力減去浮力和阻力的合力的作用,使顆粒呈加速運動。在這一階段中,隨著顆粒速度的增大而使阻力增大。當阻力增大到重力、浮力與阻力成平衡時,轉為第二階段的等速運動。此等速段的速度稱為沉降速度,也稱自由沉降速度。沉降速度就是加速階段終了時顆粒相對於流體的速度,因此也稱為終端速度,用U。表示。
由於工業上沉降操作所處理的顆粒往往很小,因此顆粒與流體問的接觸表面相對甚大,故阻力隨速度增長很快,可在短時間內便與重力、浮力相平衡。所以在重力沉降過程中,加速段常常可以忽略不計。
對於一定的顆粒與一定的流體,重力與浮力都是恆定的。令顆粒的密度為ρ,直徑為d,在粘度為μ,密度為ρ的流體中所受的力如下:
重力
浮力
合力
由力F的作用使顆粒呈加速降落(時)或加速上升(時)。
顆粒沉降達到等速運動時所受的靜力為零,因此有:
故:
式中為曳力係數,是顆粒雷諾數的函數,所以為了計算,需將兩式聯立求解。根據的不同,曳力係數與顆粒雷諾數的關係可分為幾個不同區域,因此沉降速度u的計算也需按不同區域進行。
層流區,
過渡區,
湍流區,
上三式為表面光滑的球形顆粒在流體中自由沉降的速度公式。一式稱斯托克斯公式。沉降操作中所涉及的顆粒直徑都很小,常在0.3以內,故此式常用。二式稱艾倫公式。三式稱牛頓公式。在層流區,由流體的粘性而引起的表面摩擦阻力佔主要地位;在湍流區,由流體在顆粒尾部出現邊界層分離而形成漩渦所引起的形體阻力佔主要地位。由牛頓公式可見,在湍流區內流體粘度μ對沉降速度已無影響。在整個範圍內隨著值的增加,表面摩擦阻力的作用逐漸減小以致消失,而形體阻力的作用逐漸增大,在過渡區,二者都不可忽略。
上述三式適用於計算多種情況下顆粒與流體在重力方向上的相對運動速度,即不僅適用於靜止流體中的運動顆粒,而且適用於運動流體中的靜止顆粒,或者是逆向運動著的流體與顆粒,以及同向運動著但各有不同速度的流體與顆粒之間相對運動速度的計算。使用上述三個自由沉降速度公式的條件是:容器的尺寸要遠遠大於顆粒的尺寸(譬如100倍以上),否則器壁會對顆粒的沉降有顯著的阻滯作用;顆粒不可過分細微,否則由於流體分子的碰撞將使顆粒發生布朗運動。
顆粒在流體中運動的阻力,前面已指出系由表面阻力與形體阻力所組成,它們顯然都與顆粒的形狀有關。顆粒形狀與球形的差異程度,可用它的球形度來表徵。
不同球形度的顆粒,具有不同的阻力係數。球形度值越小,顆粒形狀與圓球的差異越大,阻力係數越大,顯然,在這種情況下,有較小的沉降速度。
對於非球形顆粒,雷諾准數中的直徑d要用顆粒的當量直徑d代替。d是與一個顆粒體積相等的圓球的直徑,即
式中,為任意形狀的一個顆粒的體積,。
下圖表示球形度與雷諾准數對沉降速度的影響。圖中的縱坐標,為不規則形狀顆粒與球形顆粒沉降速度的比值,橫坐標為雷諾准數。圖中斜線表示不同球形度顆粒的關係線。由圖可見,當相同時,值越小,則值也越小。
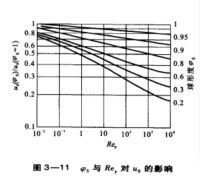
雷諾准數、球形度對沉降速度影響
以上所討論的,是單一顆粒在流體中自由沉降時的情況。但是,如果系統中顆粒濃度增大,由於顆粒的下沉和流體向上置換,發生流體動力作用的相互影響,或者發生顆粒間的相互碰撞。這種情況稱為干擾沉降。干擾沉降速度比自由沉降速度小,因為這時顆粒等於是在有效密度與有效粘度都比清液為大的懸浮體系中沉降,受到的浮力與阻力都比較大。另一方面,粒子群向下運動時,流體被置換向上,從而阻滯了鄰近的其他顆粒的沉降。
容器器壁對顆粒沉降的阻滯作用稱為壁面效應,以壁面效應因子表示, 的定義是實際沉降速度與自由沉降速度之比。 的關聯式如下:
層流:
湍流:
